Giải SBT Toán 11 CTST Bài 3. Đường thẳng và mặt phẳng song song có đáp án

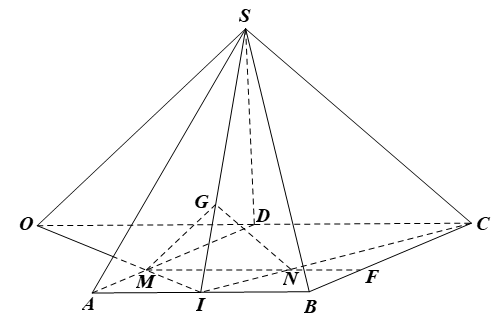
Gọi M, N lần lượt là trung điểm của DB, DC.

Xét ∆DBC có M, N lần lượt là trung điểm của DB, DC nên MN là đường trung bình của ∆DBC, suy ra MN // BC.

Do G₁ là trọng tâm ∆ABD nên $\frac{A{G}_1}{AM}=\frac{2}{3};$

      G₂ là trọng tâm ∆ACD nên $\frac{A{G}_2}{AN}=\frac{2}{3}.$

Do đó $\frac{A{G}_1}{AM}=\frac{A{G}_2}{AN}=\frac{2}{3}.$

Trong tam giác AMN, ta có $\frac{A{G}_1}{AM}=\frac{A{G}_2}{AN}=\frac{2}{3}$  nên G₁G₂ // MN (định lí Thalès đảo)

Mà MN // BC (chứng minh trên)

Suy ra G₁G₂ // MN // BC, mà BC ⊂ (ABC), MN ⊂ (BCD).

Suy ra G₁G₂ song song với các mặt phẳng (ABC) và (BCD).

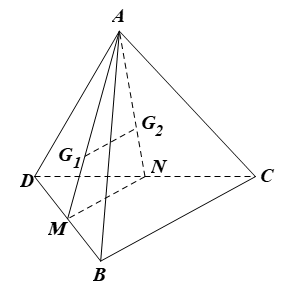
a) Do O, O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O là trung điểm của BD, AC và O’ là trung điểm của BF, AE.

Xét trong ∆BDF có: O, O’ lần lượt là trung điểm của BD, BF nên OO’ là đường trung bình của ∆BDF, suy ra OO’ // DF (1)

Tương tự, trong ∆ACE ta cũng có OO’ // CE (2)

Từ (1) và (2) suy ra OO’ // DF // CE, mà DF ⊂ (ADF), CE ⊂ (BCE)

Suy ra OO’ song song với các mặt phẳng (ADF) và (BCE).

b) Do  $AM=\frac{1}{3}AF,$  $AN=\frac{1}{3}AD$nên $\frac{AM}{AF}=\frac{AN}{AD}=\frac{1}{3}$

Xét ∆ADF có  $\frac{AM}{AF}=\frac{AN}{AD}$  suy ra MN // DF (định lý Thalès đảo)

Mà DF ⊂ (DCEF), suy ra MN // (DCEF).

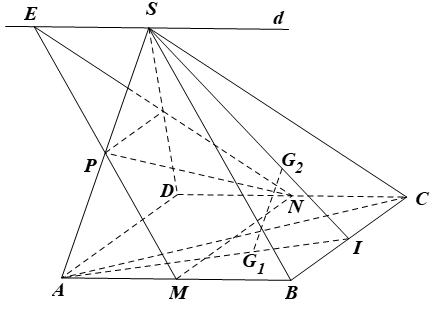
a) Hình bình hành ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD nên MN // AD // BC

Ta có MN // BC và BC ⊂ (SBC), suy ra MN // (SBC);

          MN // AD và AD ⊂ (SAD), suy ra MN // (SAD).

Vậy MN song song với các mặt phẳng (SBC) và (SAD).

b) Trong ∆SAB, có P, M lần lượt là trung điểm của SA, AB nên PM là đường trung bình, suy ra PM // SB

Mà PM ⊂ (MNP), suy ra SB // (MNP).

c) Trong mặt phẳng (SAB) vẽ đường thẳng d đi qua S và song song AB.

Gọi E là giao điểm của MP và d.

Ta có d // AB hay ES // AB, mà AB // CD nên ES // DC, tức là ES // NC (1)

Ta cũng có ES // MB và EM // SB nên MBSE là hình bình hành, suy ra ES = MB

Mà MB = NC (do M, N lần lượt là trung điểm của AB, DC và AB = DC)

Suy ra ES = NC (2)

Từ (1) và (2) suy ra ESCN là hình bình hành nên SC // NE.

Lại có NE ⊂ (MNP), suy ra SC // (MNP).

d) Gọi I là trung điểm của BC.

Do G₁ và G₂ theo thứ tự là trọng tâm của ∆ABC và ∆SBC nên $\frac{I{G}_1}{IA}=\frac{I{G}_2}{IS}=\frac{1}{3}$

Trong ∆SIA, ta có $\frac{I{G}_1}{IA}=\frac{I{G}_2}{IS}=\frac{1}{3},$  suy ra G₁G₂ // SA (định lí Thalès đảo)

Mà SA ⊂ (SAD), nên G₁G₂ // (SAD).

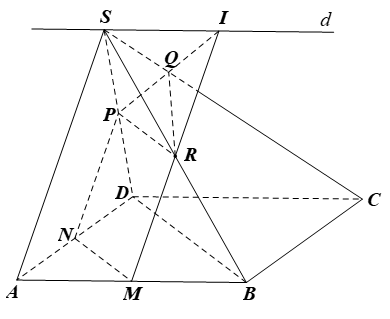
Gọi N, P, R lần lượt là trung điểm của AD, SD, SB.

Xét ∆ABD có M, N lần lượt là trung điểm của AB, AD nên MN là đường trung bình của tam giác. Do đó MN // BD.

Ta có MN // BD và MN ⊂ (MNPR) nên BD // (MNPR)

Tương tự, ta cũng có SA // (MNPR)

Ta thấy (MNPR) đi qua M và song song với BD, và SA nên chính là mp(α).

Trong mặt phẳng (SAB) vẽ đường thẳng d đi qua S và d // AB // CD.

Khi đó, giả sử MR cắt d tại I, PI cắt SC tại Q.

Lúc này, mặt phẳng (α) là (MNPI).

Ta có MN ⊂ (ABCD), MN ⊂ (MNPI) nên (MNPI) ∩ (ABCD) = MN hay (α) ∩ (ABCD) = MN.

Tương tự, (α) ∩ (SAD) = NP, (α) ∩ (SCD) = PQ, (α) ∩ (SBC) = QR, (α) ∩ (SAB) = MR.