Chuyên đề Toán 11 CTST Bài tập cuối chuyên đề 1 có đáp án
37 người thi tuần này 4.6 4.5 K lượt thi 18 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: B
Ta đặt A’(x’; y’) là ảnh của điểm A qua phép đối xứng trục Oy.
Suy ra Oy là đường trung trực của đoạn AA’.
Do đó hai điểm A(3; 5) và A’ có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ điểm A’(–3; 5).
Vậy ta chọn phương án B.
Lời giải
Đáp án đúng là: D
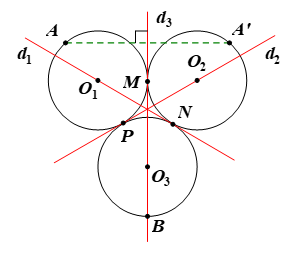
Gọi (O1), (O2), (O3) là ba đường tròn thỏa mãn yêu cầu bài toán.
Gọi M, N, P lần lượt là tiếp điểm của các cặp đường tròn (O1) và (O2); (O2) và (O3); (O1) và (O3) (hình vẽ).
Chọn các đường thẳng d1, d2, d3 lần lượt là các đường thẳng đi qua các cặp điểm O1 và N; O2 và P; O3 và M.
Lấy điểm A nằm trên hình ℋ nhưng không nằm trên đường thẳng d3.
Ta đặt A’ là ảnh của A qua phép đối xứng trục d3.
Khi đó A’ nằm trên hình ℋ ban đầu.
Lấy điểm B nằm trên hình ℋ và nằm trên đường thẳng d3.
Ta thấy B là ảnh của chính nó qua phép đối xứng trục d3.
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình ℋ, ta cũng xác định được ảnh của điểm đó qua phép đối xứng trục d3 trên hình ℋ.
Do đó phép đối xứng trục d3 biến hình ℋ thành chính nó.
Vì vậy d3 là trục đối xứng của hình ℋ.
Chứng minh tương tự với hai đường thẳng d1, d2, ta được d1, d2 cũng là trục đối xứng của hình ℋ.
Vậy hình ℋ có 3 trục đối xứng là các đường thẳng d1, d2, d3.
Do đó ta chọn phương án D.
Lời giải
Đáp án đúng là: C
Chọn điểm M(2; 0) ∈ d.
Ta đặt M’ = ĐO(M).
Suy ra O là trung điểm MM’.
Do đó
Vì vậy M’(–2; 0).
Đường thẳng d: x = 2 có vectơ pháp tuyến .
Gọi đường thẳng d’ là ảnh của đường thẳng d qua ĐO.
Suy ra đường thẳng d’ song song hoặc trùng với d nên d’ có vectơ pháp tuyến .
Vậy đường thẳng d’ đi qua M’(–2; 0) và nhận làm vectơ pháp tuyến nên có phương trình là:
1.(x + 2) + 0.(y – 0) = 0 ⇔ x + 2 = 0 ⇔ x = –2.
Do đó ta chọn phương án C.
Lời giải
Đáp án đúng là: B

Giả sử (H) là hình gồm hai đường tròn phân biệt có cùng bán kính (O; R) và (O’; R).
Gọi I là trung điểm của đoạn OO’.
Suy ra O’ = ĐI(O).
Gọi A là điểm bất kì trên (O; R).
Lấy điểm A’ sao cho I là trung điểm của AA’. Khi đó A’ = ĐI(A).
Dễ dàng chứng minh được DOAI = DO’A’I (c.g.c)
Suy ra OA = O’A’ (hai cạnh tương ứng)
Mà OA = R nên O’A’ = R hay A’ nằm trên (O’; R).
Khi đó ta luôn xác định được một điểm A’ trên hình (H) sao cho A’ = ĐI(A).
Tương tự như vậy, ta chọn các điểm khác bất kì trên hình (H), ta đều xác định được ảnh của các điểm đó qua ĐI trên hình (H).
Vì vậy I là tâm đối xứng của hình (H).
Với mỗi điểm M bất kì sao cho M ≠ I, ta luôn có MO ≠ MO’.
Do đó O’ không phải là ảnh của O qua ĐM.
Vậy hình gồm hai đường tròn phân biệt có cùng bán kính có 1 tâm đối xứng duy nhất là trung điểm của đoạn nối tâm.
Do đó ta chọn phương án B.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.