Câu hỏi:
13/07/2024 144
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Tính khoảng cách từ A đến mặt phẳng (A'BC).
Cho hình lăng trụ tam giác đều ABC.A'B'C' có tất cả các cạnh bằng a. Tính khoảng cách từ A đến mặt phẳng (A'BC).
Câu hỏi trong đề:
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
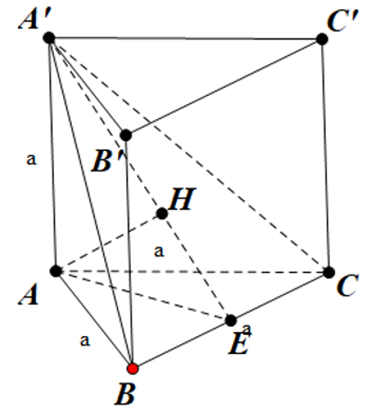
Gọi E là trung điểm của BC.
Ta có: \(\left\{ \begin{array}{l}A'E \bot BC\\AE \bot BC\end{array} \right. \Rightarrow \left( {A'AE} \right) \bot \left( {A'BC} \right)\)
Kẻ đường cao AH (H Î A'E) Þ AH ^ (A'BC)
Þ d(A, (A'BC)) = AH
\( = \sqrt {\frac{{A'{A^2}\,.\,A{E^2}}}{{A'{A^2} + A{E^2}}}} = \sqrt {\frac{{{a^2}\,.\,{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}{{{a^2} + {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}} = \frac{{a\sqrt {21} }}{7}\).
Vậy khoảng cách từ A đến mặt phẳng (A'BC) bằng \(\frac{{a\sqrt {21} }}{7}\).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm m để y = x3 − 3x2 + mx − 1 có hai điểm cực trị x1, x2 thỏa mãn x12 + x22 = 3.
Tìm m để y = x3 − 3x2 + mx − 1 có hai điểm cực trị x1, x2 thỏa mãn x12 + x22 = 3.
Xem đáp án »
13/07/2024
10,056
Câu 4:
Tìm giá trị nhỏ nhất của hàm số \(y = 3 + \sqrt {{x^2} - 2x + 5} \).
Tìm giá trị nhỏ nhất của hàm số \(y = 3 + \sqrt {{x^2} - 2x + 5} \).
Xem đáp án »
13/07/2024
5,264
Câu 5:
Cho hàm số: y = 3 − 5sin x, giá trị lớn nhất và nhỏ nhất của hàm số là M và m. Tính \(\frac{M}{m}\).
Cho hàm số: y = 3 − 5sin x, giá trị lớn nhất và nhỏ nhất của hàm số là M và m. Tính \(\frac{M}{m}\).
Xem đáp án »
13/07/2024
4,776
Câu 6:
Cho hàm số y = −x3 − mx2 + (4m + 9)x + 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng (−∞; +∞)?
Cho hàm số y = −x3 − mx2 + (4m + 9)x + 5 với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng (−∞; +∞)?
Xem đáp án »
13/07/2024
4,093
Câu 7:
Có ba lớp học sinh 10A, 10B, 10C gồm 128 em cùng tham gia lao động trồng cây. Mỗi em lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. Mỗi em lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả 3 lớp trồng được 476 cây bạch đàn và 375 cây bàng. Hỏi mỗi lớp có bao nhiêu học sinh?
Có ba lớp học sinh 10A, 10B, 10C gồm 128 em cùng tham gia lao động trồng cây. Mỗi em lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. Mỗi em lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả 3 lớp trồng được 476 cây bạch đàn và 375 cây bàng. Hỏi mỗi lớp có bao nhiêu học sinh?
Xem đáp án »
13/07/2024
3,153
về câu hỏi!