Cho hình chóp S.ABCD, cạnh đáy ABCD là nửa lục giác đều nội tiếp đường tròn có đường kính AB = 2a, SA vuông góc với hai mặt phẳng (ABCD) và \(SA = a\sqrt 3 \). Tính góc giữa hai mặt phẳng (SBC) và (SCD).

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

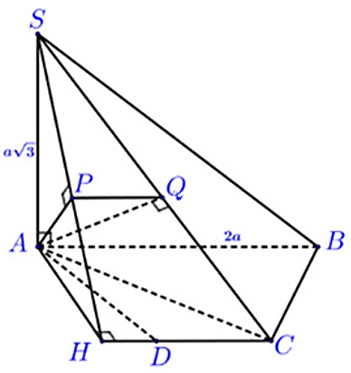
Cho hình chóp S.ABCD, cạnh đáy ABCD là nửa lục giác đều nội tiếp đường tròn có (ảnh 1)

Ta có ABCD là nửa lục giác đều suy ra AD = DC = CB = a

Dựng đường thẳng đi qua điểm A và vuông góc với mặt phẳng (SCD)

Trong (ABCD) dựng AH ^ CD tại H suy ra CD ^ (SAH)

Trong (SAH) dựng AP ^ SH Þ CD ^ AP Þ AP ^ (SCD)

Tiếp tục dựng đường thẳng đi qua A và vuông góc với mặt phẳng (SBC)

Trong (SAC) dựng đường AQ ^ SC

Vì BC ^ AC, BC ^ SA Þ BC ^ (SAC) Þ BC ^ AQ

Þ AQ ^ SBC)

Do đó góc giữa hai mặt phẳng (SBC), (SCD) là góc giữa hai đường thẳng vuông góc lần lượt với hai mặt phẳng là AP và AQ.

Ta có: ∆SAC vuông cân tại A suy ra \(AQ = \frac{{SC}}{2} = \frac{{a\sqrt 6 }}{2}\)

Mặt khác ∆AQP vuông tại O suy ra

\(\cos \widehat {PAQ} = \frac{{AP}}{{AQ}} = \frac{{\sqrt {10} }}{5} \Rightarrow \widehat {PAQ} = \arccos \frac{{\sqrt {10} }}{5}\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm m để y = x³ − 3x² + mx − 1 có hai điểm cực trị x₁, x₂ thỏa mãn x₁² + x₂² = 3.

Xem đáp án

Lời giải

Ta có: y¢ = 3x² − 6x + m

Để hàm số có hai điểm cực trị khi và chỉ khi phương trình y¢ = 0 có 2 nghiệm phân biệt

Û ∆¢ = 9 − 3m > 0 Û m < 3

Khi đó theo hệ thức Vi-ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = \frac{m}{3}\end{array} \right.\)

Theo bài ra ta có: x₁² + x₂² = 3

Û (x₁ + x₂)² − 2x₁x₂ = 3

\( \Leftrightarrow {2^2} - \frac{{2m}}{3} = 3\)

\( \Leftrightarrow m = \frac{3}{2}\) (thỏa mãn)

Vậy \(m = \frac{3}{2}\) là giá trị cần tìm.

Câu 2

Có ba lớp học sinh 10A, 10B, 10C gồm 128 em cùng tham gia lao động trồng cây. Mỗi em lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. Mỗi em lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả 3 lớp trồng được 476 cây bạch đàn và 375 cây bàng. Hỏi mỗi lớp có bao nhiêu học sinh?

Xem đáp án

Lời giải

Gọi x, y, z (học sinh) lần lượt là số học sinh của lớp 10A, 10B, 10C (x, y, z ∈ ℕ*).

Điều kiện x, y, z nguyên dương.

Ba lớp học sinh 10A, 10B, 10C gồm 128 em nên ta có phương trình x + y + z = 128.

Mỗi em lớp 10A trồng được 3 cây bạch đàn, mỗi em lớp 10B trồng được 2 cây bạch đàn, mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả 3 lớp trồng được 476 cây bạch đàn nên ta có phương trình 3x + 2y + 6z = 476

Mỗi em lớp 10A trồng được 4 cây bàng, mỗi em lớp 10B trồng được 5 cây bàng. Cả 3 lớp trồng được 375 cây bàng nên ta có phương trình 4x + 5y = 375.

Từ đó ta có hệ phương trình

\(\left\{ \begin{array}{l}x + y + z = 128\\3x + 2y + 6z = 476\\4x + 5y = 375\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y - 3z = - 92\\ - y + 4z = 137\\x + y + z = 128\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}z = 45\\y = 43\\x = 40\end{array} \right.\)

Vậy 10A có 40 học sinh, 10B có 43 học sinh, 10C có 45 học sinh.

Câu 3