Cho hình lập phương ABCD có cạnh là 2. Gọi M, N lần lượt là trung điểm của BC và CD. Tính diện tích thiết diện của hình lập phương khi cắt bởi mặt phẳng (A'MN).

Xem lời giải

Câu hỏi trong đề: 7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

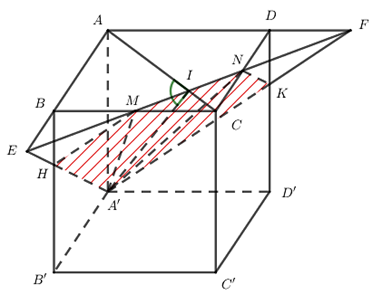
Cho hình lập phương ABCD có cạnh là 2. Gọi M, N lần lượt là trung điểm của BC (ảnh 1)

Kéo dài MN cắt AB và AD lần lượt tại E và F.

Gọi H = A'E Ç BB'; K = A'F Ç DD'. Khi đó thiết diện là A'HMNK.

Ta có ABMND là hình chiếu của A’HMNK trên mặt phẳng (ABCD).

Gọi I = AC Ç MN. ta có: AC ^ BD; MN // BD Þ AC ^ MN tại I.

\(\left\{ \begin{array}{l}MN \bot AI\\MN \bot AA'\end{array} \right. \Rightarrow MN \bot \left( {A'AI} \right) \Rightarrow MN \bot A'I\)

\( \Rightarrow \left( {\widehat {\left( {A'HMNK} \right);\;\left( {ABCD} \right)}} \right) = \widehat {AIA'}\)

Ta có:

• \(CM = CN = 1 \Rightarrow MN = \sqrt 2 \Rightarrow IC = \frac{{\sqrt 2 }}{2}\)

• \(AC = 2\sqrt 2 \Rightarrow AI = 2\sqrt 2 - \frac{{\sqrt 2 }}{2} = \frac{{3\sqrt 2 }}{2}\)

Xét tam giác vuông AA'I có:

\(A'I = \sqrt {AA{'^2} + A{I^2}} = \sqrt {{2^2} + {{\left( {\frac{{3\sqrt 2 }}{2}} \right)}^2}} = \frac{{\sqrt {34} }}{2}\)

\( \Rightarrow \cos \widehat {AIA'} = \frac{{AI}}{{A'I}} = \frac{{\frac{{3\sqrt 2 }}{2}}}{{\frac{{\sqrt {34} }}{2}}} = \frac{3}{{\sqrt {17} }} = \cos \left( {\widehat {\left( {A'HMNK} \right);\;\left( {ABCD} \right)}} \right)\)

Ta có: \({S_{ABCD}} = 4;\;{S_{CMN}} = \frac{1}{2}\,.\,1\,.\,1 = \frac{1}{2}\)

\( \Rightarrow {S_{ABMND}} = 4 - \frac{1}{2} = \frac{7}{2}\).

\( \Rightarrow {S_{A'HMNK}} = \frac{{{S_{ABMND}}}}{{\cos \widehat {AIA'}}} = \frac{7}{2}\,.\,\frac{{\sqrt {17} }}{3} = \frac{{7\sqrt {17} }}{6}\).

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm m để y = x³ − 3x² + mx − 1 có hai điểm cực trị x₁, x₂ thỏa mãn x₁² + x₂² = 3.

Xem đáp án

Lời giải

Ta có: y¢ = 3x² − 6x + m

Để hàm số có hai điểm cực trị khi và chỉ khi phương trình y¢ = 0 có 2 nghiệm phân biệt

Û ∆¢ = 9 − 3m > 0 Û m < 3

Khi đó theo hệ thức Vi-ét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = \frac{m}{3}\end{array} \right.\)

Theo bài ra ta có: x₁² + x₂² = 3

Û (x₁ + x₂)² − 2x₁x₂ = 3

\( \Leftrightarrow {2^2} - \frac{{2m}}{3} = 3\)

\( \Leftrightarrow m = \frac{3}{2}\) (thỏa mãn)

Vậy \(m = \frac{3}{2}\) là giá trị cần tìm.

Câu 2

Có ba lớp học sinh 10A, 10B, 10C gồm 128 em cùng tham gia lao động trồng cây. Mỗi em lớp 10A trồng được 3 cây bạch đàn và 4 cây bàng. Mỗi em lớp 10B trồng được 2 cây bạch đàn và 5 cây bàng. Mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả 3 lớp trồng được 476 cây bạch đàn và 375 cây bàng. Hỏi mỗi lớp có bao nhiêu học sinh?

Xem đáp án

Lời giải

Gọi x, y, z (học sinh) lần lượt là số học sinh của lớp 10A, 10B, 10C (x, y, z ∈ ℕ*).

Điều kiện x, y, z nguyên dương.

Ba lớp học sinh 10A, 10B, 10C gồm 128 em nên ta có phương trình x + y + z = 128.

Mỗi em lớp 10A trồng được 3 cây bạch đàn, mỗi em lớp 10B trồng được 2 cây bạch đàn, mỗi em lớp 10C trồng được 6 cây bạch đàn. Cả 3 lớp trồng được 476 cây bạch đàn nên ta có phương trình 3x + 2y + 6z = 476

Mỗi em lớp 10A trồng được 4 cây bàng, mỗi em lớp 10B trồng được 5 cây bàng. Cả 3 lớp trồng được 375 cây bàng nên ta có phương trình 4x + 5y = 375.

Từ đó ta có hệ phương trình

\(\left\{ \begin{array}{l}x + y + z = 128\\3x + 2y + 6z = 476\\4x + 5y = 375\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y - 3z = - 92\\ - y + 4z = 137\\x + y + z = 128\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}z = 45\\y = 43\\x = 40\end{array} \right.\)

Vậy 10A có 40 học sinh, 10B có 43 học sinh, 10C có 45 học sinh.

Câu 3