Cho hình hộp ABCD.A'B'CD' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60°. Tính khoảng cách giữa hai đường thẳng AB' và A'C'
Cho hình hộp ABCD.A'B'CD' có tất cả các cạnh đều bằng 1 và các góc phẳng đỉnh A đều bằng 60°. Tính khoảng cách giữa hai đường thẳng AB' và A'C'
A. \(\frac{{\sqrt {22} }}{{11}}\).
B. \(\frac{2}{{11}}\).
C. \(\frac{{\sqrt 2 }}{{11}}\).
D. \(\frac{3}{{11}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
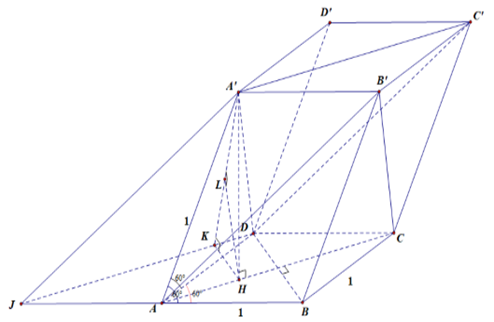
Ta có \(\widehat {BAA'} = \widehat {DAA'} = \widehat {BAD} = {60^ \circ }\) và AB = AD = AA’.
Khi đó ∆ABD, ∆ADA’ và ∆ABA’ và ∆ABA’ đều cạnh bằng 1 .
⇒ A’D = A’A = A’B = 1. Suy ra hình chiếu của A’ lên (ABCD) là tâm H của ∆ABD đều.
Ta có AB’ // DC’ ⇒ d(AB’; A’C’) = d(AB’; (DA’C’)) = d(H; (DA’C’)).
Dựng hình bình hành DCAJ. Từ H kẻ HK ⊥ DJ (K ∈ DJ), ta có HK // DB.
Từ H kẻ HL ⊥ A’K (L ∈ A’K) ⇒ HL ⊥ (DA’C’) ⇒ d(H; (DA’C’)) = HL.
Ta có: \(HK = \frac{1}{2},A'H = \sqrt {1 - {{\left( {\frac{{\sqrt 3 }}{3}} \right)}^2}} = \frac{{\sqrt 6 }}{3}\).
Xét tam giác \(A'HK:\frac{1}{{H{L^2}}} = \frac{1}{{H{K^2}}} + \frac{1}{{A'{H^2}}} \Rightarrow HL = \frac{{\sqrt {22} }}{{11}}\).
Đáp án cần chọn là: A.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 41811.
B. 42802.
C. 56875.
D. 32023.
Lời giải
Đáp án đúng là: C
Ta có các trường hợp sau
TH 1: Đề thi gồm 2D, 3TB, 1K:\(C_{15}^2 \cdot C_{10}^2 \cdot C_5^1.\)
TH 2: Đề thi gồm 2D, 1TB, 2K:\(C_{15}^2 \cdot C_{10}^1 \cdot C_5^2.\)
TH 3: Đề thi gồm 3D, 1TB, 1K:\(C_{15}^3 \cdot C_{10}^1 \cdot C_5^1.\)
Vậy có: \(C_{15}^2 \cdot C_{10}^2 \cdot C_5^1 + C_{15}^2 \cdot C_{10}^1 \cdot C_5^2 + C_{15}^3 \cdot C_{10}^1 \cdot C_5^1 = 56875\) đề kiểm tra.
Đáp án cần chọn là: C
Câu 2
A. 227 người/km2.
B. 722 người/km2.
C. 277 người/km2.
D. 272 người/km2.
Lời giải
Đáp án đúng là: D
Công thức tính: Mật độ dân số = tổng số dân / tổng diện tích (người/km2)
- Áp dụng công thức:
Đổi 331212 km2 = 0,331212 triệu km2
Mật độ dân số =90/0,331212 = 271,7 (người/km2)
Làm tròn kết quả ta được: mật độ dân số nước ta là 272 người/km2.
Đáp án cần chọn là: D
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(y' = \frac{{x \cdot {2^{1 + {x^2}}}}}{{{\rm{ln}}2}}.\)
B. \(y' = x \cdot {2^{1 + {x^2}}} \cdot {\rm{ln}}2.\)
C. \(y' = {2^x} \cdot {\rm{ln}}{2^x}.\)
D. \(y' = \frac{{x \cdot {2^{1 + x}}}}{{{\rm{ln}}2}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. min F = 1 khi x = 2; y = 3.
B. min F =2 khi x = 0; y = 2.
C. min F = 3 khi x = 1; y = 4.
D. min F = 0 khi x = 0; y = 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. (‒1; 1).
B. (1; 0).
C. (0; 1).
D. (1; 1).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[\frac{5}{6}.\]
B. \[\frac{{611}}{{715}}.\]
C. \[\frac{{600}}{{713}}.\]
D. \[\frac{6}{7}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo