Câu hỏi:
13/07/2024 4,947
Một chất điểm có khối lượng \(100{\rm{\;g}}\) dao động điều hoà trên quỹ đạo là đoạn thẳng \({\rm{MN}}\) (dài hơn \(8{\rm{\;cm}}\)). Tại điểm \({\rm{P}}\) cách \({\rm{M}}\) một khoảng \(4{\rm{\;cm}}\) và tại điểm \({\rm{Q}}\) cách \({\rm{N}}\) một khoảng \(2{\rm{\;cm}}\), chất điểm có động năng tương ứng là \({32.10^{ - 3}}{\rm{\;J}}\) và \({18.10^{ - 3}}{\rm{\;J}}\). Tính tốc độ trung bình khi vật đi từ \({\rm{P}}\) đến \({\rm{Q}}\).
Một chất điểm có khối lượng \(100{\rm{\;g}}\) dao động điều hoà trên quỹ đạo là đoạn thẳng \({\rm{MN}}\) (dài hơn \(8{\rm{\;cm}}\)). Tại điểm \({\rm{P}}\) cách \({\rm{M}}\) một khoảng \(4{\rm{\;cm}}\) và tại điểm \({\rm{Q}}\) cách \({\rm{N}}\) một khoảng \(2{\rm{\;cm}}\), chất điểm có động năng tương ứng là \({32.10^{ - 3}}{\rm{\;J}}\) và \({18.10^{ - 3}}{\rm{\;J}}\). Tính tốc độ trung bình khi vật đi từ \({\rm{P}}\) đến \({\rm{Q}}\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Tốc độ tại P: \({v_P} = \sqrt {\frac{{2{W_{dP}}}}{m}} = 80{\rm{\;cm/s}}\); tại Q: \({v_Q} = \sqrt {\frac{{2{W_{dQ}}}}{m}} = 60{\rm{\;cm/s}}\).
Do \({v_P} > {v_Q}\) nên li độ \(\left| {{x_P}} \right| < \left| {{x_Q}} \right|:\left\{ {\begin{array}{*{20}{l}}{\left| {{x_P}} \right| = A - 4}\\{\left| {{x_Q}} \right| = A - 2}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{l}}{v_P^2 = {\omega ^2}\left( {{A^2} - x_P^2} \right)}\\{v_Q^2 = {\omega ^2}\left( {{A^2} - x_Q^2} \right)}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{v_P^2 = 8{\omega ^2}\left( {A - 2} \right)}\\{v_Q^2 = 4{\omega ^2}\left( {A - 1} \right)}\end{array}} \right.} \right.\)
Giải hệ ta được: \(A = 10{\rm{\;cm}}\) và \(\omega = 10{\rm{rad}}/{\rm{s}}\).
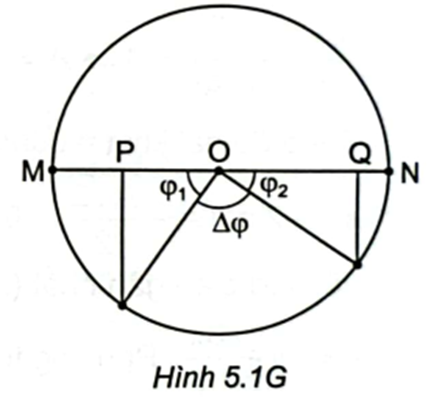
Quãng đường \(PQ = OP + OQ\)\( = \left( {A - 4} \right) + \left( {A - 2} \right) = 14{\rm{\;cm}}{\rm{.\;}}\)
Thời gian vật đi từ P đến Q là \({\rm{\Delta }}t\) với: \({\rm{\Delta }}t = \frac{{{\rm{\Delta }}\varphi }}{\omega }\).
\({\rm{\Delta }}\varphi = \pi - \left( {{\varphi _1} + {\varphi _2}} \right) = \frac{\pi }{2}\), với \({\rm{cos}}{\varphi _1} = \frac{{{\rm{OP}}}}{{\rm{A}}};{\rm{cos}}{\varphi _2} = \frac{{{\rm{OQ}}}}{{\rm{A}}} \Rightarrow {\rm{\Delta t}} = \frac{{\rm{T}}}{4} = \frac{\pi }{{20}}\)
\( \Rightarrow \) Tốc độ trung bình khi vật đi từ P đến Q: \(\overline v = \frac{{PQ}}{{{\rm{\Delta }}t}} = \frac{{14}}{{\frac{\pi }{{20}}}} \approx 89{\rm{\;cm/s}}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
\(\frac{{{F_{{\rm{max}}}}}}{{{F_{{\rm{min}}}}}} = \frac{{k\left( {{\rm{\Delta }}{l_0} + A} \right)}}{{k\left( {{\rm{\Delta }}{l_0} - A} \right)}} = \frac{7}{3} \Rightarrow 3\left( {{\rm{\Delta }}{l_0} + A} \right) = 7\left( {{\rm{\Delta }}{l_0} - A} \right)\)\( \Rightarrow {\rm{\Delta }}{l_0} = 2,5{\rm{\;A}} = 25{\rm{\;cm}} = 0,25{\rm{\;m}}\).
Với \({\rm{\Delta }}{l_0}\) là độ dãn của lò xo tại vị trí cân bằng.
\(\omega = \sqrt {\frac{g}{{{\rm{\Delta }}{l_0}}}} = \sqrt {\frac{{10}}{{0,25}}} = 2\pi \left( {{\rm{rad}}/{\rm{s}}} \right) \Rightarrow f = \frac{\omega }{{2\pi }} = 1{\rm{\;Hz}}\).
Lời giải
Đáp án đúng là A
Thời gian giữa năm lần liên tiếp động năng bằng thế năng là:
\(4 \cdot \frac{T}{4} = 0,4 \Rightarrow T = 0,4{\rm{\;s}} \Rightarrow f = \frac{1}{{0,4}} = 2,5{\rm{\;Hz}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 22: Cường độ dòng điện có đáp án
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 16: Lực tương tác giữa các điện tích có đáp án
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 23: Điện trở. Định luật Ôm có đáp án
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 24: Nguồn điện có đáp án
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 25: Năng lượng. Công suất điện có đáp án
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 1: Dao động điều hòa có đáp án
-
Đề thi cuối kì 2 Vật lí 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 18: Điện trường đều có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận