Câu hỏi:
13/07/2024 7,179
Tại một điểm \({\rm{O}}\) trên mặt nước có một nguồn dao động điều hoà theo phương thẳng đứng với tần số \(2{\rm{\;Hz}}\). Từ điểm \({\rm{O}}\) có những gợn sóng tròn lan rộng ra xung quanh. Khoảng cách giữa hai gợn sóng kế tiếp là \(20{\rm{\;cm}}\). Tốc độ truyền sóng trên mặt nước là
A. \(20{\rm{\;cm}}/{\rm{s}}\).
B. \(40{\rm{\;cm}}/{\rm{s}}\).
C. 80 cm/s.
D. 120cm/s
Tại một điểm \({\rm{O}}\) trên mặt nước có một nguồn dao động điều hoà theo phương thẳng đứng với tần số \(2{\rm{\;Hz}}\). Từ điểm \({\rm{O}}\) có những gợn sóng tròn lan rộng ra xung quanh. Khoảng cách giữa hai gợn sóng kế tiếp là \(20{\rm{\;cm}}\). Tốc độ truyền sóng trên mặt nước là
A. \(20{\rm{\;cm}}/{\rm{s}}\).
B. \(40{\rm{\;cm}}/{\rm{s}}\).
C. 80 cm/s.
D. 120cm/s
Câu hỏi trong đề: Giải SBT Vật lý 11 KNTT Mô tả sóng có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là B
Khoảng cách giữa hai gợn sóng bằng 1 bước sóng nên \[\lambda = 20\,cm\]
Tốc độ truyền sóng: \[v = \lambda f = 20.2 = 40\,cm/s\]
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Vì sóng tại hai điểm A, B ngược pha nhau, nên khoảng cách AB thoả mãn:
\(AB = d = \left( {2k + 1} \right)\frac{\lambda }{2} = \left( {2k + 1} \right)\frac{v}{{2f}} \Rightarrow v = \frac{{2fd}}{{2k + 1}} = \frac{{16}}{{2k + 1}}\), với \(k \in Z\).
Theo đề bài: \(3{\rm{\;m}}/{\rm{s}} \le {\rm{v}} \le 5{\rm{\;m}}/{\rm{s}} \Rightarrow 3 \le \frac{{16}}{{2k + 1}} \le 5 \Leftrightarrow 1,1 \le k \le 2,17\)
Vậy \(k = 2\). Suy ra tốc độ truyền sóng là: \(v = \frac{{16}}{{2k + 1}} = \frac{{16}}{{2 \cdot 2 + 1}} = \frac{{16}}{5} = 3,2{\rm{\;m/s}}\).
Lời giải
Đáp án đúng là A
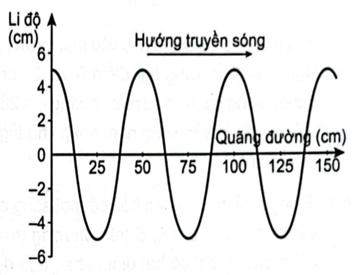
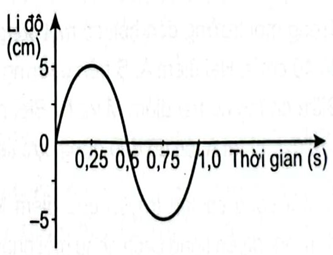
Biên độ sóng là 5 cm, bước sóng là 50 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 22: Cường độ dòng điện có đáp án
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 23: Điện trở. Định luật Ôm có đáp án
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 1: Dao động điều hòa có đáp án
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 16: Lực tương tác giữa các điện tích có đáp án
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 24: Nguồn điện có đáp án
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 25: Năng lượng. Công suất điện có đáp án
-
Đề thi cuối kì 2 Vật lí 11 Kết nối tri thức cấu trúc mới có đáp án - Đề 1
-
10 câu Trắc nghiệm Vật lí 11 Kết nối tri thức Bài 17: Khái niệm điện trường có đáp án