Câu hỏi:
13/11/2023 5,338
Số lượng học sinh tham gia Câu lạc bộ Cờ vua của một trường được biểu diễn ở biểu đồ sau:
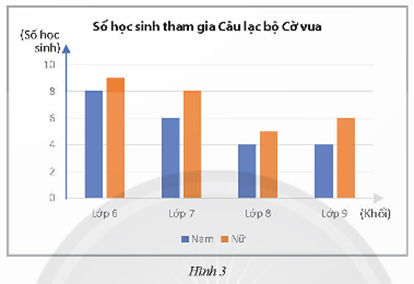
Chọn ngẫu nhiên 1 học sinh trong Câu lạc bộ Cờ vua của trường đó. Tính xác suất của các biến cố:
A: "Học sinh được chọn là nữ";
B: "Học sinh được chọn học lớp 8";
C: "Học sinh được chọn là nam và không học lớp 7".
Số lượng học sinh tham gia Câu lạc bộ Cờ vua của một trường được biểu diễn ở biểu đồ sau:
Chọn ngẫu nhiên 1 học sinh trong Câu lạc bộ Cờ vua của trường đó. Tính xác suất của các biến cố:
A: "Học sinh được chọn là nữ";
B: "Học sinh được chọn học lớp 8";
C: "Học sinh được chọn là nam và không học lớp 7".
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
Số học sinh tham gia Câu lạc bộ Cờ vua là 50 học sinh.
Số học sinh nữ tham gia Câu lạc bộ Cờ vua là:
9 + 8 + 5 + 6 = 28 (học sinh).
Khi đó, số kết quả thuận lợi của biến cố A là 28.
Xác suất biến cố A là: \(P\left( A \right) = \frac{{28}}{{50}} = \frac{{14}}{{25}}\).
Số học sinh lớp 8 tham gia Câu lạc bộ Cờ vua là:
4 + 5 = 9 (học sinh)
Khi đó, số kết quả thuận lợi của biến cố B là 9.
Xác suất biến cố B là: \(P\left( B \right) = \frac{9}{{50}}\).
Số học sinh nam không học lớp 7 tham gia Câu lạc bộ Cờ vua là:
8 + 4 + 4 = 16 (học sinh)
Khi đó, số kết quả thuận lợi của biến cố C là 16.
Xác suất biến cố C là: \(P(C) = \frac{{16}}{{50}} = \frac{8}{{25}}\).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
- Có 6 kết quả có thể xảy ra là: 1; 2; 3; 4; 5; 6.
- Vì con xúc xắc là cân đối và đồng chất nên 6 kết quả có cùng xác suất xảy ra là \(\frac{1}{6}\).
- Có 2 kết quả thuận lợi cho biến cố A là: 3; 6.
Vậy xác suất biến cố A là: \(P\left( A \right) = \frac{2}{6} = \frac{1}{3}\).
Lời giải
Lời giải:
Các viên bi có kích thước và khối lượng bằng nhau nên có khả năng xảy ra bằng nhau.
Ta có tổng số bi trong hộp là: 3 + 4 + 5 = 12 (viên)
Vì có 3 viên bi màu xanh nên số kết quả thuận lợi cho biến cố A là: 3.
Xác suất của biến cố A là: \(P\left( A \right) = \frac{3}{{12}} = \frac{1}{4}\)
Vì có 4 viên bi màu đỏ nên số kết quả thuận lợi cho biến cố B là: 12 – 4 = 8.
Xác suất của biến cố B là: \(P\left( B \right) = \frac{8}{{12}} = \frac{2}{3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
10 Bài tập Nhận biết đơn thức, đơn thức thu gọn, hệ số, phần biến và bậc của đơn thức (có lời giải)
-
Dạng 8: Bài luyện tập 3 dạng 4. Tổng hợp có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
-
Dạng 2: Bài luyện tập 1 Dạng 2: Rút gọn phân thức có đáp án