Giải SBT Toán 8 CTST Mô tả xác suất bằng tỉ số có đáp án

• Các kết quả thuận lợi cho biến cố A là 5; 10; 15; 20.

• Các kết quả thuận lợi cho biến cố B là 1; 2; 3; 4; 6; 8; 12.

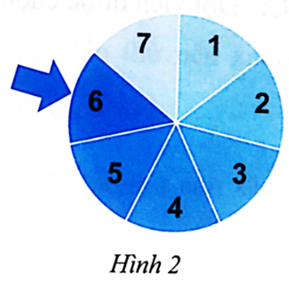
• Các kết quả thuận lợi cho biến cố A là ô ghi số 4, ô ghi số 5, ô ghi số 6, ô ghi số 7.

• Các kết quả thuận lợi cho biến cố B là ô ghi số 1, ô ghi số 3, ô ghi số 5, ô ghi số 7.

Tổng số viên bi trong hộp là: 6 + 4 = 10 (viên bi).

• Trong hộp có 4 viên bi màu xanh nên xác suất xảy ra biến cố A là:

\(P\left( A \right) = \frac{4}{{10}} = 0,4\).

• Trong hộp có 6 viên bi màu đỏ nên xác suất xảy ra biến cố B là:

\[P\left( B \right) = \frac{6}{{10}} = 0,6\].

• Trong hộp không có bi màu vàng nên biến cố C không xảy ra.

Khi đó, xác suất xảy ra biến cố C là P(C) = 0.

Bác Minh phải thử chữ số cuối cùng bằng cách chọn 1 trong 10 chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8; 9.

Vậy xác suất để bác Minh mở được điện thoại là \(\frac{1}{{10}} = 0,1\).

Số học sinh trong nhóm là:

2 + 4 + 4 + 6 = 16 (bạn).

• Có 4 bạn quê ở Cần Thơ nên xác suất xảy ra biến cố A là:

\(P\left( A \right) = \frac{4}{{16}} = 0,25\).

• Các bạn ở Hà Giang và Hà Nội ở miền Bắc.

Do đó số bạn ở miền Bắc trong nhóm là: 2 + 6 = 8 (bạn).

Xác suất xảy ra biến cố B là: \(P\left( B \right) = \frac{8}{{16}} = 0,5\).

Vậy xác suất của biến cố A là 0,25 và xác suất của biến cố B là 0,5.

Gọi số quả bóng màu đỏ là n. Tổng số quả bóng trong hộp là n + 20 (quả).

Trong hộp có 20 quả bóng màu xanh nên xác suất của biến cố “Quả bóng lấy ra có màu xanh” là \(\frac{{20}}{{n + 20}}\).

Theo đề bài, xác suất của biến cố “Quả bóng lấy ra có màu xanh” là 0,4 nên ta có

\(\frac{{20}}{{n + 20}} = 0,4\)

n + 20 = 50

n = 30.

Vậy trong hộp có 30 quả bóng màu đỏ.

Tổng số đội viên trong đội giao lưu là:

5 + 7 + 7 + 5 + 5 + 6 + 8 + 7 = 50 (đội viên).

• Có 7 đội viên học lớp 5 trường Tiểu học Kim Đồng nên xác suất xảy ra biến cố A là:

\(P\left( A \right) = \frac{7}{{50}} = 0,14\).

• Số đội viên học trường Tiểu học Đoàn Kết là:

7 + 5 = 12 (đội viên).

Xác suất xảy ra biến cố B là: \(P\left( B \right) = \frac{{12}}{{50}} = 0,24\).

• Số đội viên học lớp 4 là:

5 + 7 + 5 + 8 = 25 (đội viên)

Xác suất xảy ra biến cố C là: \(P\left( C \right) = \frac{{25}}{{50}} = 0,5\).

Vậy xác suất của các biến cố A là 0,14; xác suất của các biến cố B là 0,24 và xác suất của các biến cố C là 0,5.