Giải SGK Toán 8 CTST Bài 4. Phân tích đa thức thành nhân tử có đáp án
53 người thi tuần này 4.6 2.1 K lượt thi 38 câu hỏi
🔥 Đề thi HOT:
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
5.7 K lượt thi
15 câu hỏi
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
2.5 K lượt thi
15 câu hỏi
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
13.7 K lượt thi
18 câu hỏi
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
2 K lượt thi
15 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 5)
3.1 K lượt thi
21 câu hỏi
Bộ 10 đề thi giữa kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án (Đề 10)
3.1 K lượt thi
15 câu hỏi
Dạng 4: Bài luyện tập 2 có đáp án
4.6 K lượt thi
13 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Ta có: 993 – 99 = 99.(992 – 1)
= 99.(992 – 12)
= 99.(99 – 1).(99 + 1)
= 99.98.100
Do đó 993 – 99 chia hết cho cả ba số 98, 99 và 100.
Ta có: n3 – n = n(n2 – 1)
= n.(n – 1).(n + 1)
Do đó n3 – n chia hết cho n, n – 1 và n + 1.
Vậy phát biểu của cả hai bạn đều đúng.
Lời giải
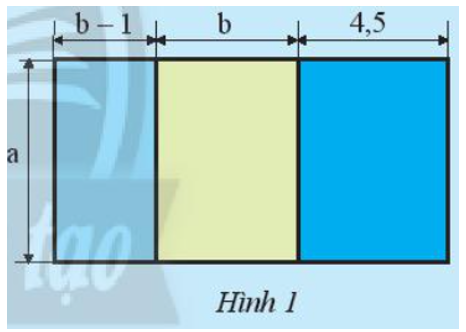
Cách 1: Tính tổng diện tích các hình.
Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng b – 1 (m) là: a(b – 1) (m2).
Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng b (m) là: ab (m2).
Diện tích hình chữ nhật có chiều dài a (m) và chiều rộng 4,5 (m) là: 4,5a (m2).
Diện tích của nền nhà là: S = a(b – 1) + ab + 4,5a (m2).
Với a = 5 và b = 3,5 ta có:
S = 5.(3,5 – 1) + 5.3,5 + 4,5.5
= 5 . (3,5 – 1 + 3,5 + 4,5)
= 5 . 10,5
= 52,5 (m2).
Cách 2: Tính chiều dài của nền nhà rồi tính diện tích của nền nhà.
Chiều dài của nền nhà là:
b – 1 + b + 4,5 = 2b + 3,5 (m).
Diện tích của nền nhà là: S = a.(2b + 3,5) (m2).
Với a = 5 và b = 3,5 ta có:
S = 5.(2.3,5 + 3,5) = 5 . 10,5 = 52,5 (m2).
Chú ý: Ngoài 2 cách trên ta có thể tính diện tích của nền nhà theo cách khác.
Trong tất cả các cách thì ta thấy Cách 2 là nhanh nhất.
Lời giải
a) P = 6x – 2x3
= 2x.3 – 2x.x2
= 2x(3 – x2).
Lời giải
b) Q = 5x3 – 15x2y
= 5x2.x – 5x2.3y
= 5x2(x – 3y).
Lời giải
c) R = 3x3y3 – 6xy3z + xy
= xy.3x2y2 – xy.6y2z + xy.1
= xy(3x2y2 – 6y2z + 1).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo