Giải SGK Toán 8 CTST Bài 1: Khái niệm hàm số có đáp án

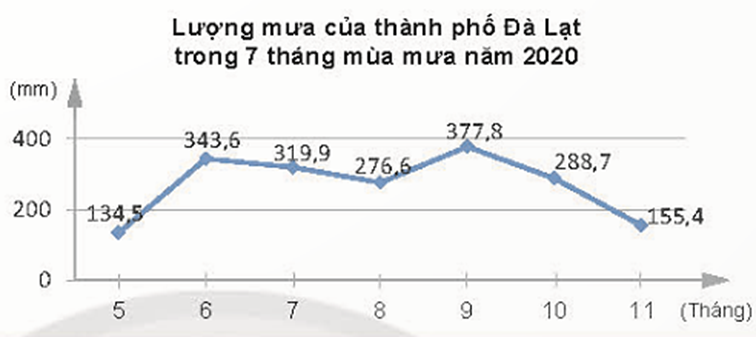
Lượng mưa tháng 5 là 134,5 mm;

Lượng mưa tháng 6 là 343,6 mm;

Lượng mưa tháng 7 là 319,9 mm;

Lượng mưa tháng 8 là 276,6 mm;

Lượng mưa tháng 9 là 377,8 mm;

Lượng mưa tháng 10 là 288,7 mm;

Lượng mưa tháng 11 là 155,4 mm.

Ứng với mỗi giờ chỉ đọc được một số chỉ nhiệt độ.

Ứng với 7h thì nhiệt độ là (36°C)

Ứng với 8h thì nhiệt độ là (37°C)

Ứng với 9h thì nhiệt độ là (36°C)

Ứng với 10h thì nhiệt độ là (37°C)

Ứng với 11h thì nhiệt độ là (38°C)

Ứng với 12h thì nhiệt độ là (37°C)

Ứng với 13h thì nhiệt độ là (38°C)

Ứng với 14h thì nhiệt độ là (39°C)

Ứng với 15h thì nhiệt độ là (39°C)

Với v = 10 $\Rightarrow t=\frac{180}{10}=18$

Với v = 20 $\Rightarrow t=\frac{180}{20}=9$

Với v = 30 $\Rightarrow t=\frac{180}{30}=6$

Với v = 60 $\Rightarrow t=\frac{180}{60}=3$

Với v = 180 $\Rightarrow t=\frac{180}{180}=1$

Ta có bảng:

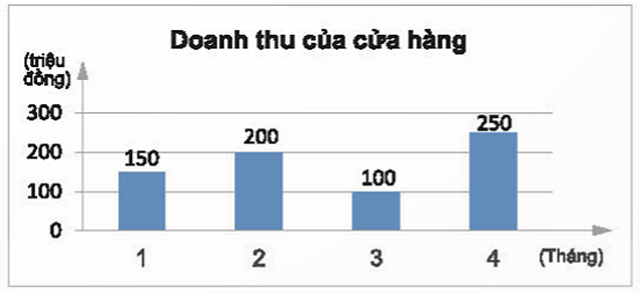
a) Đại lượng là hàm số là doanh thu y (triệu đồng) của một cửa hàng và biến số là tháng x.

b) Đại lượng là hàm số là quãng đường s (km) đi được và biến số là thời gian t (giờ).

c) Đại lượng là hàm số là số tiền y (đồng) người mua phải trả và biến số là số x quyển vở.

F là một hàm số theo biến C vì với mỗi giá trị của C chỉ cho ta duy nhất một giá trị của F.

a) Với x = 4 ta có: y = 2.4 + 3 = 11

b) Với x = 10 ta có: y = 10.4 + 3 = 43.

Ta có bảng sau:

Với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y nên đại lượng y là hàm số của đại lượng x.

f(2) = 2² = 4; f(−3) = (−3)² = 9.

Ta có f(0) = 0² = 0; f(−1) = (−1)² = 1;

f(2) = 2² = 4; f(3) = 3² = 9.

Từ đó ta có bảng:

Ta có: C = $\mathrm{\pi }$d trong đó, C là chu vi đường tròn; d là đường kính và p là số pi.

Do đó, f(d) = $\mathrm{\pi }$.d

Với d = 1 ⇒ f(1) = $\mathrm{\pi }$.1 = $\mathrm{\pi }$

d = 2 ⇒ f(2) = $\mathrm{\pi }$.2 = 2$\mathrm{\pi }$

d = 3 ⇒ f(3) = $\mathrm{\pi }$.3 = 3$\mathrm{\pi }$

d = 4 ⇒ f(4) = $\mathrm{\pi }$.4 = 4$\mathrm{\pi }$

Ta thu được bảng sau:

Dựa vào bảng, ta thấy với một giá trị của x ta chỉ nhận được một giá trị của y tương ứng, do đó đại lượng y là hàm số của đại lượng x.

Dựa vào bảng, ta thấy tồn tại một giá trị của x ta có thể nhận được hai giá trị của y tương ứng, do đó đại lượng y không là hàm số của đại lượng x.

Ví dụ: Khi x = 2 thì y = $\frac{1}{2}$ hoặc y = $\frac{1}{3}$

Ta có:

• f(1) = 3.1 = 3;

• f(−2) = 3.(−2) = −6;

• $f\left(\frac{1}{3}\right)=3.\frac{1}{3}=1$

Ta có f(−3) = 3.(−3) = −9; f(−1) = 3.(−1) = −3;

f(0) = 3.0 = 0; f(2) = 3.2 = 6; f(3) = 3.3 = 9.

Từ đó ta có bảng sau:

• f(−3) = (−3)² + 4 = 9 + 4 = 13;

• f(−2) = (−2)² + 4 = 4 + 4 = 8;

• f(−1) = (−1)² + 4 = 5;

• f(0) = 0 + 4 = 4;

• f(1) = 1 + 4 = 5.

Vậy f(−3) = 13; f(−2) = 8; f(−1) = 5; f(0) = 4; f(1) = 5.

Đại lượng m là hàm số của đại lượng V vì với mỗi một giá trị của V ta luôn chỉ xác định được một giá trị của m.

Ta có: m = 7,8V

m(10) = 7,8.10 = 78;

m(20) = 7,8.20 = 156;

m(40) = 7,8.40 = 312;

m(50) = 7,8.50 = 390.

• Với v = 10 ta có $t=\frac{20}{10}=2$

• Với v = 20 ta có $t=\frac{20}{20}=1$;

• Với v = 40 ta có $t=\frac{20}{40}=0,5$;

• Với v = 80 ta có $t=\frac{20}{80}=0,25$.

Khi đó, ta có bảng sau: