Giải SBT Toán 8 CTST Hai tam giác đồng dạng có đáp án
35 người thi tuần này 4.6 668 lượt thi 11 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 10 (có đáp án)
Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 1
Bài tập ôn tập Toán 8 Chương 8 (có đáp án)
Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 2
Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 1
Danh sách câu hỏi:
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
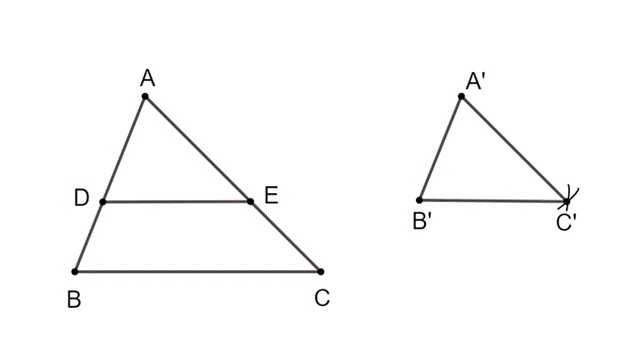
Trên cạnh AB lấy điểm D sao cho \[AD = \frac{3}{5}AB\].
Từ D kẻ đường thẳng song song với BC và cắt AC tại E.
Ta có ∆ADE ᔕ ∆ABC theo tỉ số đồng dạng \[k = \frac{{AD}}{{AB}} = \frac{3}{5}\].
Dựng ∆A’B’C’ = ∆ADE.
Dựng A’B’ = AD.
Dựng cung tròn tâm A’ bán kính AE và cung tròn tâm B’ bán kính DE, hai cung tròn cắt nhau tại C’.
Nối B’C’, A’C’ ta được tam giác phải dựng.
Ta có ∆ADE ᔕ ∆ABC theo tỉ số\[k = \frac{3}{5}\] nên ∆A’B’C’ ᔕ ∆ABC theo tỉ số \[k = \frac{3}{5}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
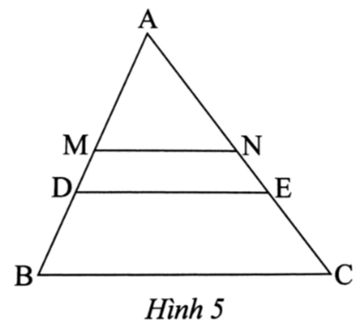
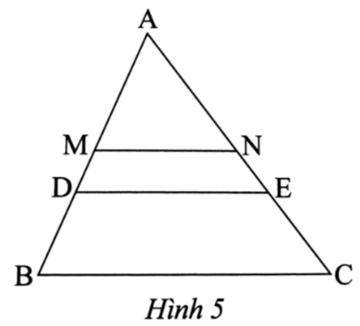
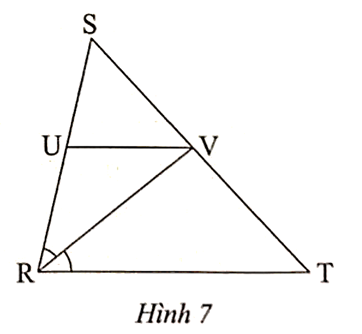
Ta có MN là đường trung bình của tam giác ABC, suy ra MN // BC.
Suy ra ∆ABC ᔕ ∆AMN. Mà ∆ADE ᔕ ∆ABC, suy ra ∆ADE ᔕ ∆AMN.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
∆ADE ᔕ ∆ABC theo tỉ số \[\frac{{AD}}{{AB}} = \frac{2}{3}\].
∆ABC ᔕ ∆AMN theo tỉ số \[\frac{{AB}}{{AM}} = 2\] (vì M là trung điểm AB).
Suy ra \[\frac{{AD}}{{AB}}.\frac{{AB}}{{AM}} = \frac{2}{3}.2 = \frac{4}{3}\] hay \[\frac{{AD}}{{AM}} = \frac{4}{3}\].
Vậy ∆ADE ᔕ ∆AMN theo tỉ số \[\frac{{AD}}{{AM}} = \frac{4}{3}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
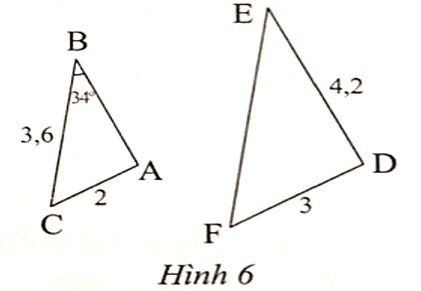
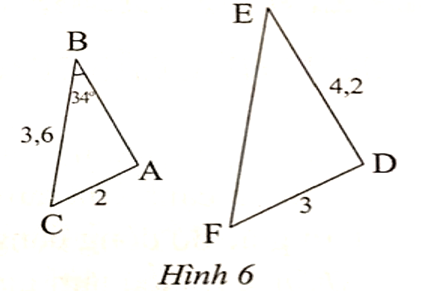
Ta có ∆ABC ᔕ ∆DEE nên \[\widehat E = \widehat B\]= 34°.
Vậy \[\widehat E = 34^\circ \].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
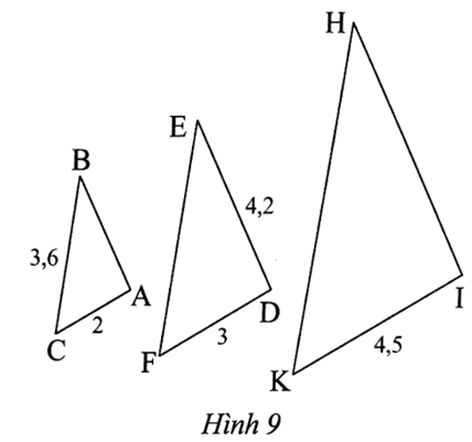
Ta có ∆ABC ᔕ ∆DEE suy ra
\[\frac{{AD}}{{DE}} = \frac{{BC}}{{EF}} = \frac{{AC}}{{DF}}\] hay \[\frac{{AB}}{{4,2}} = \frac{{3,6}}{{EF}} = \frac{2}{3}\].
Suy ra \[\frac{{AB}}{{4,2}} = \frac{2}{3}\] và \[\frac{{3,6}}{{EF}} = \frac{2}{3}\].
Do đó \[AB = \frac{{2.4,2}}{3} = 2,8\] và \[EF = \frac{{3,6.3}}{2} = 5,4\].
Vậy AB = 2,8 và EF = 5,4.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có UV // RT suy ra ∆SUV ᔕ ∆SRT.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 5/11 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập