Trong Hình 5, cho biết MN là đường trung bình của tam giác ABC. Tam giác ADE đồng dạng với tam giác ABC theo tỉ số \[k = \frac{2}{3}\].
Tính tỉ số đồng dạng của ∆ADE và ∆AMN.
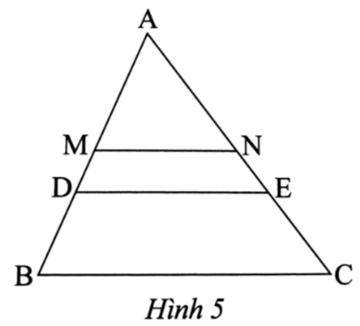
Trong Hình 5, cho biết MN là đường trung bình của tam giác ABC. Tam giác ADE đồng dạng với tam giác ABC theo tỉ số \[k = \frac{2}{3}\].
Tính tỉ số đồng dạng của ∆ADE và ∆AMN.

Câu hỏi trong đề: Giải SBT Toán 8 CTST Hai tam giác đồng dạng có đáp án !!
Quảng cáo
Trả lời:
∆ADE ᔕ ∆ABC theo tỉ số \[\frac{{AD}}{{AB}} = \frac{2}{3}\].
∆ABC ᔕ ∆AMN theo tỉ số \[\frac{{AB}}{{AM}} = 2\] (vì M là trung điểm AB).
Suy ra \[\frac{{AD}}{{AB}}.\frac{{AB}}{{AM}} = \frac{2}{3}.2 = \frac{4}{3}\] hay \[\frac{{AD}}{{AM}} = \frac{4}{3}\].
Vậy ∆ADE ᔕ ∆AMN theo tỉ số \[\frac{{AD}}{{AM}} = \frac{4}{3}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
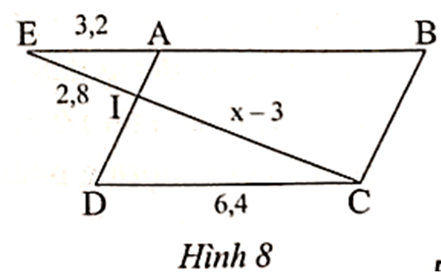
Ta có AE // DC (ABCD là hình bình hành).
Suy ra ∆IAE ᔕ ∆IDC, suy ra \[\frac{{IE}}{{IC}} = \frac{{AE}}{{DC}}\] hay \[\frac{{2,86}}{{x - 3}} = \frac{{3,2}}{{6,4}}\].
Khi đó x – 3 = 5,6, suy ra x = 5,6 + 3 = 8,6.
Vậy x = 8,6.
Lời giải
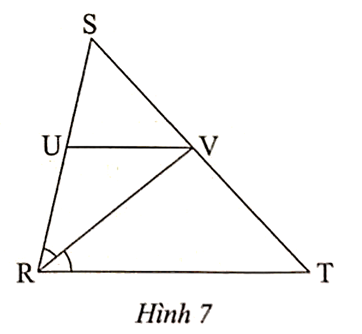
Ta có \[\widehat {RVU} = \widehat {VRT}\] (so le trong), \[\widehat {URV} = \widehat {VRT}\] (RV là tia phân giác \[\widehat {SRT}\]).
Suy ra \[\widehat {RVU} = \widehat {URV}\] nên ∆RUV cân tại U. Do đó UR = UV.
Mà \[\frac{{SU}}{{SR}} = \frac{{UV}}{{RT}}\] (∆SUV ᔕ ∆SRT). Suy ra\[\frac{{SU}}{{UR}} = \frac{{SR}}{{RT}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.