Giải SBT Toán 8 CTST Đường trung bình của tam giác có đáp án

31 người thi tuần này 4.6 690 lượt thi 12 câu hỏi

Đề số 1

🔥 Học sinh cũng đã học

693 người thi tuần này

Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 2

2 K lượt thi 11 câu hỏi

452 người thi tuần này

Đề kiểm tra Toán 8 Chương 10 (có đáp án) - Đề 1

1.8 K lượt thi 11 câu hỏi

233 người thi tuần này

Bài tập ôn tập Toán 8 Chương 10 (có đáp án)

537 lượt thi 50 câu hỏi

115 người thi tuần này

Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 2

677 lượt thi 11 câu hỏi

167 người thi tuần này

Đề kiểm tra Toán 8 Chương 8 (có đáp án) - Đề 1

729 lượt thi 11 câu hỏi

140 người thi tuần này

Bài tập ôn tập Toán 8 Chương 8 (có đáp án)

431 lượt thi 50 câu hỏi

103 người thi tuần này

Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 2

638 lượt thi 11 câu hỏi

162 người thi tuần này

Đề kiểm tra Toán 8 Chương 9 (có đáp án) - Đề 1

697 lượt thi 11 câu hỏi

Danh sách câu hỏi:

Câu 1/12

Cho tam giác nhọn ABC có M, N lần lượt là trung điểm của AB, AC.

Chứng minh tứ giác BMNC là hình thang.

Xem đáp án

Lời giải

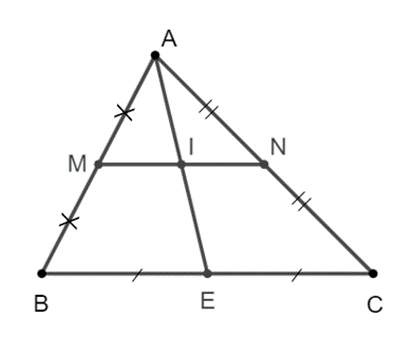
Chứng minh tứ giác BMNC là hình thang (ảnh 1)

Xét ∆ABC, ta có MA = MB và NA = NC, nên MN là đường trung bình của ∆ABC.

Suy ra MN // BC.

Tứ giác BMNC có MN // BC nên BMNC là hình thang.

Câu 2/12

Cho tam giác nhọn ABC có M, N lần lượt là trung điểm của AB, AC.

Gọi E là trung điểm của BC và I là giao điểm của AE với MN. Chứng minh I là trung điểm của MN.

Xem đáp án

Lời giải

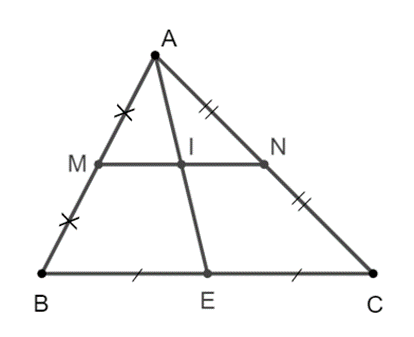
Gọi E là trung điểm của BC và I là giao điểm của AE với MN. Chứng minh I là (ảnh 1)

Xét ∆ABE, ta có MA = MB và MI // BE (vì I ∈ MN, E ∈ BC) nên IA = IE.

Do đó MI là đường trung bình của ∆ABE, suy ra MI = \[\frac{{BE}}{2}\].

Tương tự, ta có IN = \[\frac{{EC}}{2}\].

Mặt khác BE = EC, suy ra MI = IN.

Vậy I là trung điểm của MN.

Câu 3/12

Cho tam giác nhọn ABC, kẻ trung tuyển AM (M ∈ BC). Gọi I là trung điểm của AM, đường thẳng CI cắt AB tại E. Từ M kẻ đường thẳng song song với CE cắt AB tại F. Chứng minh:

EF = FB;

Xem đáp án

Lời giải

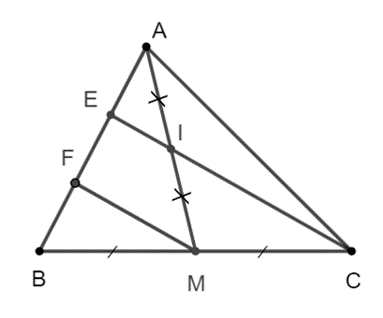
Xét ∆BCE, ta có MB = MC và MF // CE nên EF = FB.

Câu 4/12

Cho tam giác nhọn ABC, kẻ trung tuyển AM (M ∈ BC). Gọi I là trung điểm của AM, đường thẳng CI cắt AB tại E. Từ M kẻ đường thẳng song song với CE cắt AB tại F. Chứng minh:

AE = \[\frac{1}{3}\]AB;

Xem đáp án

Lời giải

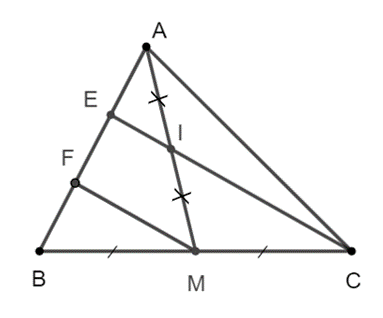
Xét ∆AMF, ta có IA = IM và EI // MF (vì I ∈ CE) nên EA = EF.

Suy ra EA = EF = FB mà EA + EF + FB = AB.

Vậy AE = \[\frac{1}{3}\]AB.

Câu 5/12

Cho tam giác nhọn ABC, kẻ trung tuyển AM (M ∈ BC). Gọi I là trung điểm của AM, đường thẳng CI cắt AB tại E. Từ M kẻ đường thẳng song song với CE cắt AB tại F. Chứng minh:

CE = 4EI.

Xem đáp án

Lời giải

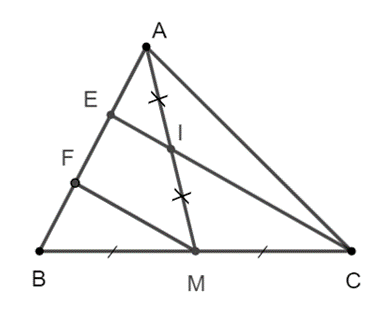
Xét ∆BCE, ta có MB = MC và EF = FB, nên MF là đường trung bình của ∆BCE.

Suy ra CE = 2MF (1)

Tương tự, có EI là là đường trung bình của ∆AMF, suy ra MF = 2EI (2)

Từ (1) và (2) suy ra CE = 4EI.

Câu 6/12

Cho tam giác ABC, hai đường trung tuyến EM và CN cắt nhau tại G (M ∈ AC, N ∈ AB). Gọi D, E lần lượt là trung điểm của GB, GC. Chứng minh:

MN // DE;

Xem đáp án

Lời giải

Xét ∆ABC, ta có MA = MC và NA = NB nên MN là đường trung bình của ∆ABC.

Suy ra MN // BC (1)

Xét ∆BCG, ta có BD = DG và CE = EG nên DE là đường trung bình của ∆BCG.

Suy ra DE // BC (2)

Từ (1) và (2) suy ra MN // DE.

Câu 7/12