Giải SBT Toán 8 CTST Bài tập cuối chương 7 có đáp án

Đáp án đúng là: B

Tỉ số của hai đường thẳng AB và CD là:

\[\frac{{AB}}{{CD}} = \frac{{12}}{{10}} = \frac{6}{5}\].

Đáp án đúng là: C

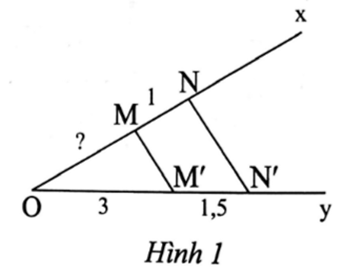
Xét ∆ONN' có MM' // NN' nên theo định lí Thalès, ta có \[\frac{{OM}}{{MN}} = \frac{{OM'}}{{M'N'}}\].

Suy ra \[OM = \frac{{MN\,.\,OM'}}{{M'N'}} = \frac{{1.\,3}}{{1,5}} = 2\] (cm).

Vậy OM = 2 cm.

Đáp án đúng là: D

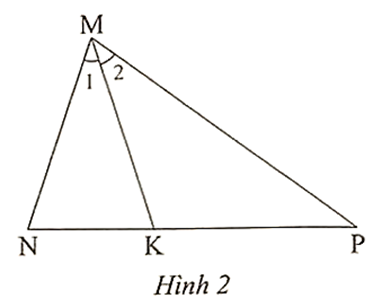
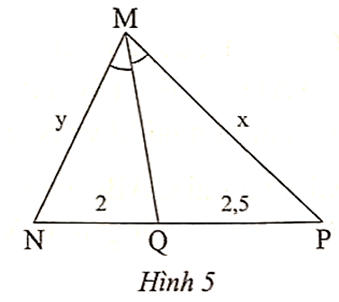
Vì MK là phân giác của \[\widehat {NMP}\] trong ∆MNP nên \[\frac{{MN}}{{MP}} = \frac{{NK}}{{KP}}\].

Do đó \[\frac{{MN}}{{NK}} = \frac{{MP}}{{KP}}\] (theo tính chất tỉ lệ thức).

Đáp án đúng là: A

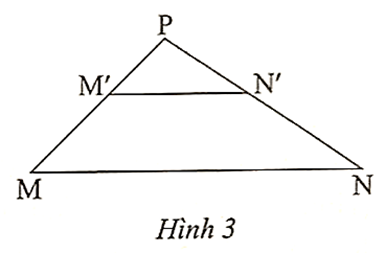
Xét ∆PMN có M'N' // MN nên theo định lí Thalès, ta có :

\[\frac{{PM'}}{{PM}} = \frac{{PN'}}{{PN}}\]; \[\frac{{PM'}}{{M'M}} = \frac{{PN'}}{{N'N}}\]; \[\frac{{M'M}}{{PM}} = \frac{{N'N}}{{PN}}\].

Đáp án đúng là: C

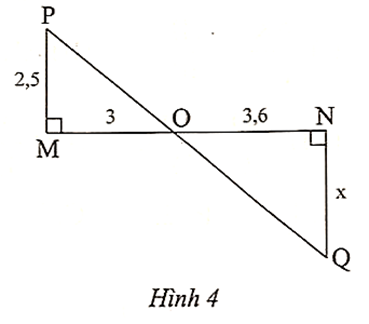
Vì MP ⊥ MN, NQ ⊥ MN nên MP // NQ.

Xét ∆OMP có MP // NQ, theo hệ quả của định lí Thalès, ta có \[\frac{{OM}}{{ON}} = \frac{{MP}}{{NQ}}\].

Do đó NQ = \[\frac{{MP.ON}}{{OM}} = \frac{{2,5.3,6}}{3} = 3\].

Vậy x = 3.

Đáp án đúng là: B

Vì MQ là tia phân giác của \[\widehat {NMP}\] trong ∆MNP nên

\[\frac{{MP}}{{MN}} = \frac{{QP}}{{QN}} = \frac{{2,5}}{2} = \frac{5}{4}\].

Vậy \[\frac{x}{y} = \frac{5}{4}\].

Đáp án đúng là: D

Vì ABCD là hình vuông và M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên

AM = MB = BN = NC = CP = PD = DQ = QA.

Suy ra AM² + QA² = MB² + BN² = NC² + CP² = PD² + DQ²,

Khi đó MQ² = MN² = NP² = PQ² hay MQ = MN = NP = PQ,

Do đó tứ giác MNPQ là hình thoi       (1)

• Vì AM = AQ nên ∆AMQ vuông cân tại A, suy ra \[\widehat {AMQ}\] = 45°.

• Vì BM = BN nên ∆BMN vuông cân tại B, suy ra \[\widehat {BMN}\] = 45°.

Mà \[\widehat {AMQ}\]+ \[\widehat {QMN}\] + \[\widehat {BMN}\] = 180°, suy ra \[\widehat {QMN}\] = 90°       (2)

Từ (1) và (2) suy ra MNPQ là hình vuông.

 S_ABCD = AB² ; S_MNPQ = MQ²

MQ² = AM² + QA² = \[{\left( {\frac{1}{2}AB} \right)^2}\]+ \[{\left( {\frac{1}{2}AD} \right)^2}\]

= \[\frac{1}{4}\]AB² + \[\frac{1}{4}\]AD² = \[\frac{1}{4}\]AB² + \[\frac{1}{4}\]AB² = \[\frac{1}{2}\]AB².

Do đó S_MNPQ = \[\frac{1}{2}\]S_ABCD.

Đáp án đúng là: B

• Xét ∆OAD có NA = ND và NQ // OD nên QO = QA = \[\frac{1}{2}\]OA.

• Xét ∆OBD có MB = MC và MP // OB nên PO = PC = \[\frac{1}{2}\]OC.

Mà ABCD là hình bình hành, suy ra OC = OA.

Do đó OQ = OP. Suy ra O là trung điểm PQ.

Đáp án đúng là: A

Vì EB = \[\frac{1}{2}\]AB; FC = \[\frac{1}{2}\]AC, AB = AC nên EB = FC = \[\frac{1}{2}\](dm)  

Xét ∆ABC có EA = EB và FA = FC nên FF là đường trung bình của ∆ABC.

Suy ra EF = \[\frac{1}{2}\]BC = \[\frac{1}{2}\](dm).

Chu vi hình thang EFCB bằng:

EF + FC + BC + EB =  \[\frac{5}{2}\](dm)

Đáp án đúng là: C

Theo hệ quả của định lí Thalès:

• Xét ∆OEC có AK // EC nên \[\frac{{AK}}{{EC}} = \frac{{BK}}{{DE}}\].

• Xét ∆OED có BK // DE nên \[\frac{{BK}}{{DE}} = \frac{{OK}}{{KE}}\].

Suy ra \[\frac{{AK}}{{EC}} = \frac{{BK}}{{DE}}\].

Mà EC = DE , suy ra AK = BK.

Xét ∆OCD có AB // CD, theo hệ quả của định lí Thalès, ta có:

\[\frac{{AO}}{{AC}} = \frac{{AB}}{{DC}} = \frac{{OB}}{{OD}}\].

Vậy có 3 khẳng định đúng là các khẳng định (I), (II), (III).

Xét ∆OAB, ta có MA = MO và NB = NO.

Suy ra MN là đường trung bình của ∆ABC nên MN = \[\frac{1}{2}\]AB.

Do đó AB = 2MN = 2.45 = 90 (m).

Vậy khoảng cách AB là 90 m.

Ta có AB ⊥ AD, EF ⊥ AD, GH ⊥ AD, DG ⊥ AD.

Suy ra AB // EF // GH // DG.

• Xét tứ giác EFCD có EF // CD nên tứ giác EFCD là hình thang.

• Xét hình thang EFCD có FH= HC và GH // EF nên EG = GD.

Do đó GH là đường trung bình của hình thang EFCD.

Suy ra \[GH = \frac{{EF + GC}}{2}\]=\[\frac{{10 + 14}}{2} = 12\].

Tương tự, có EF là đường trung bình của hình thang ABHG.

Suy ra \[EF = \frac{{AB + GH}}{2}\], suy ra AB = 2EF – GH = 2.10 – 12 = 8.

Vậy x = 8 và y = 12.