Giải SGK Toán 8 CTST Bài 1. Mô tả xác suất bằng tỉ số có đáp án

Lời giải:

Các kết quả khi lấy ngẫu nhiên 1 thẻ từ hộp là: 3; 4; 5; 6; 7; 8; 9; 10; 11; 12.

• Các số ghi trên thẻ chia hết cho 3 là: 3; 6; 9; 12.

Do đó, các kết quả làm cho mỗi biến cố sau xảy ra làm cho biến cố A xảy ra là: 3; 6; 9; 12.

• Các số ghi trên thẻ chia hết cho 6 là: 6; 12.

Do đó, các kết quả làm cho mỗi biến cố sau xảy ra làm cho biến cố B xảy ra là: 6; 12.

Lời giải:

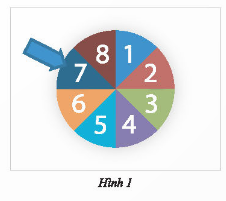
Ta có các kết quả có thể xảy ra khi mũi tên chỉ vào một trong những ô số trên là:

1; 2; 3; 4; 5; 6; 7; 8.

• Các ô ghi số chẵn là: 2; 4; 6; 8.

Do đó, các kết quả thuận lợi cho biến cố A là: 2; 4; 6; 8.

• Các ô ghi số chia hết cho 4 là: 4; 8.

Do đó, các kết quả thuận lợi cho biến cố B là: 4; 8.

• Các ô ghi số nhỏ hơn 3 là: 1; 2.

Do đó, các kết quả thuận lợi cho biến cố C là: 1; 2.

Lời giải:

a) Vì gặp ngẫu nhiên một người trong 200 người nên 200 kết quả có khả năng xảy ra như nhau.

Số người làm Kinh doanh trong 200 người ở khu phố là:

200.24% = 48 (người)

Số người làm Y tế trong 200 người ở khu phố là:

200.12% = 24 (người)

Số người làm Giáo dục trong 200 người ở khu phố là:

200.10% = 20 (người)

Số người làm Sản xuất trong 200 người ở khu phố là:

200.30% = 60 (người)

Số người làm Dịch vụ trong 200 người ở khu phố là:

200.24% = 48 (người)

a) Gọi A là biến cố người gặp ngẫu nhiên là người làm trong lĩnh vực giáo dục.

Biến cố A xảy ra khi người gặp ngẫu nhiên là người làm trong lĩnh vực giáo dục do đó, số kết quả thuận lợi của biến cố A là 20. Xác suất của biến cố A là:

\(P(A) = \frac{{20}}{{200}} = \frac{1}{{10}}\).

Vậy xác suất người đó có công việc thuộc lĩnh vực Giáo dục là \(\frac{1}{{10}}\).

b) Gọi B là biến cố người gặp ngẫu nhiên không thuộc lĩnh vực Y tế hay Dịch vụ.

Khi đó, người gặp ngẫu nhiên có thể thuộc lĩnh vực Kinh doanh, Giáo dục hoặc Sản xuất.

Biến cố B xảy ra khi người gặp ngẫu nhiên là người làm trong lĩnh vực Kinh doanh, Giáo dục hoặc Sản xuất do đó, số kết quả thuận lợi của biến cố B là:

48 + 20 + 60 = 128.

Xác suất của biến cố B là:

\(P(B) = \frac{{128}}{{200}} = \frac{{16}}{{25}}\).

Vậy xác suất người đó có công việc không thuộc lĩnh vực Y tế hay Dịch vụ là \(\frac{{16}}{{25}}\).

Lời giải:

Các quả bóng có kích thước và khối lượng bằng nhau nên có khả năng xảy ra bằng nhau.

Có 2 kết quả thuận lợi cho biến cố A là: 5; 13.

Xác suất của biến cố A là: \(P\left( A \right) = \frac{2}{5}\).

Có 0 kết quả thuận lợi cho biến cố B hay biến cố B là biến cố không thể suy ra P(B) = 0.

Có 5 kết quả thuận lợi cho biến cố C là: 5; 8; 10; 13; 16. Hay C là biến cố chắc chắn nên P(C) = 1.

Lời giải:

Các viên bi có kích thước và khối lượng bằng nhau nên có khả năng xảy ra bằng nhau.

Ta có tổng số bi trong hộp là: 3 + 4 + 5 = 12 (viên)

Vì có 3 viên bi màu xanh nên số kết quả thuận lợi cho biến cố A là: 3.

Xác suất của biến cố A là: \(P\left( A \right) = \frac{3}{{12}} = \frac{1}{4}\)

Vì có 4 viên bi màu đỏ nên số kết quả thuận lợi cho biến cố B là: 12 – 4 = 8.

Xác suất của biến cố B là: \(P\left( B \right) = \frac{8}{{12}} = \frac{2}{3}\).

Lời giải:

Số học sinh tham gia Câu lạc bộ Cờ vua là 50 học sinh.

Số học sinh nữ tham gia Câu lạc bộ Cờ vua là:

9 + 8 + 5 + 6 = 28 (học sinh).

Khi đó, số kết quả thuận lợi của biến cố A là 28.

Xác suất biến cố A là: \(P\left( A \right) = \frac{{28}}{{50}} = \frac{{14}}{{25}}\).

Số học sinh lớp 8 tham gia Câu lạc bộ Cờ vua là:

4 + 5 = 9 (học sinh)

Khi đó, số kết quả thuận lợi của biến cố B là 9.

Xác suất biến cố B là: \(P\left( B \right) = \frac{9}{{50}}\).

Số học sinh nam không học lớp 7 tham gia Câu lạc bộ Cờ vua là:

8 + 4 + 4 = 16 (học sinh)

Khi đó, số kết quả thuận lợi của biến cố C là 16.

Xác suất biến cố C là: \(P(C) = \frac{{16}}{{50}} = \frac{8}{{25}}\).

Lời giải:

a) Số học sinh thuộc khối 9 là: 24% . 600 = 144 (học sinh)

Xác suất của biến cố "Học sinh được chọn thuộc khối 9" là: \(\frac{{144}}{{600}} = \frac{6}{{25}}\).

b) Số học sinh thuộc khối 6 là: 28% . 600 = 168 (học sinh)

Số học sinh không thuộc khối 6 là: 600 – 168 = 432 (học sinh)

Xác suất của biến cố "Học sinh được chọn không thuộc khối 6" là: \(\frac{{432}}{{600}} = \frac{{18}}{{25}}\).