1. Lớp 8
  2. Toán
  3. Giải SGK Toán 8 CTST Bài 2. Đường trung bình của tam giác có đáp án

Giải SGK Toán 8 CTST Bài 2. Đường trung bình của tam giác có đáp án

81 người thi tuần này 4.6 1.2 K lượt thi 18 câu hỏi

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Bài giảng / Lý thuyết:

Toán Lớp 8 Bài 2 Đường trung bình của tam giác - Trang 52, 54 - Chân trời sáng tạo | Tập 2

🔥 Học sinh cũng đã học

Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 10

0 lượt thi x câu hỏi

Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 05

0 lượt thi 15 câu hỏi

Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 04

0 lượt thi 15 câu hỏi

Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 03

0 lượt thi 15 câu hỏi

Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 02

0 lượt thi 15 câu hỏi

Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức có đáp án - Đề 01

0 lượt thi 15 câu hỏi
152 người thi tuần này

Bộ 5 đề thi cuối kì 2 Toán 8 Chân trời sáng tạo (Tự luận) có đáp án - Đề 5

535 lượt thi 5 câu hỏi
65 người thi tuần này

Bộ 5 đề thi cuối kì 2 Toán 8 Chân trời sáng tạo (Tự luận) có đáp án - Đề 4

448 lượt thi 5 câu hỏi

Danh sách câu hỏi:

Câu 1

Giữa hai điểm B và C có một hồ nước (xem hình bên). Biết DE = 45 m. Làm thế nào để tính được khoảng cách giữa hai điểm B và C?

Giữa hai điểm B và C có một hồ nước (xem hình bên). Biết DE = 45 m. Làm thế nào để tính được khoảng cách giữa hai điểm B và C? (ảnh 1)

Lời giải

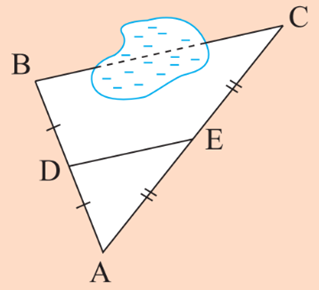
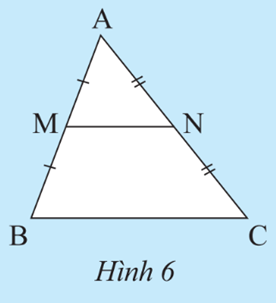
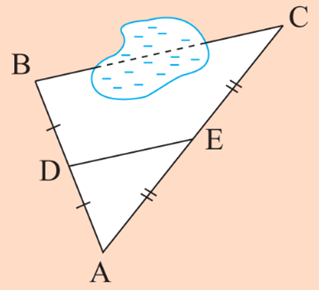
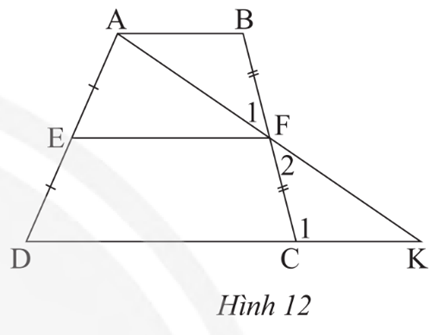
Xét tam giác ABC, ta có: 

ADAB=AEAC=12

Theo định lí Thalès đảo, ta có DE // BC.

Suy ra DEBC=ADAB=12 , vậy BC = 2DE = 90 m.

Sau khi học xong bài này:

Ta có: D, E là trung điểm của AB và AC nên DE là đường trung bình của tam giác ABC suy ra DE=12BC vậy BC = 2DE = 90 m.

Câu 2

Cho tam giác ABC, vẽ đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N (Hình 1). Hãy chứng minh N là trung điểm của AC

Cho tam giác ABC, vẽ đường thẳng d đi qua trung điểm M của cạnh AB, song song với cạnh BC và cắt AC tại N (Hình 1). Hãy chứng minh N là trung điểm của AC. (ảnh 1)

Lời giải

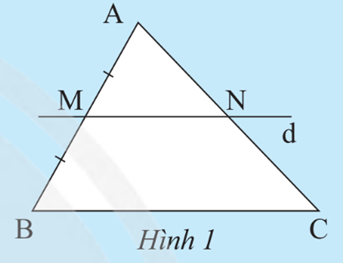
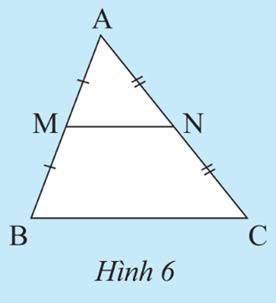
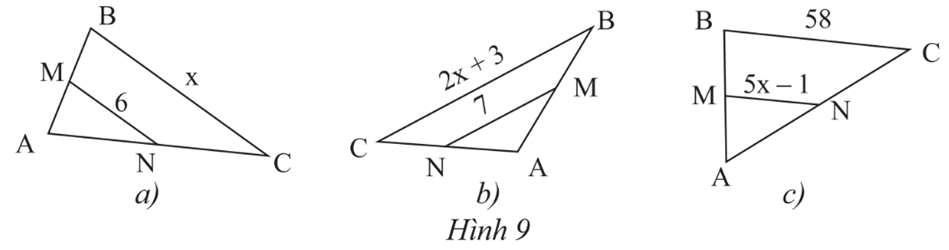
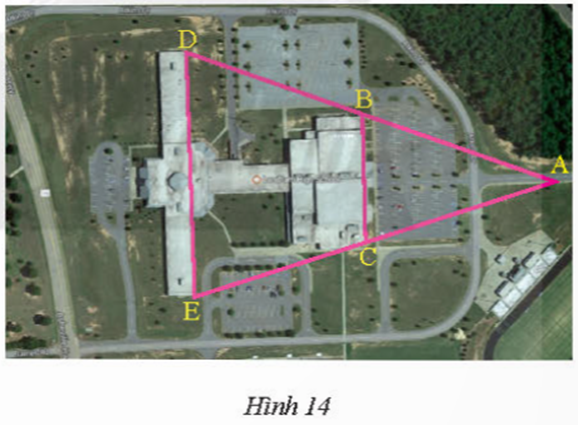
Xét tam giác ABC có MN // BC, theo định lí Thalès, ta có: AMAB=ANAC=12

Suy ra N là trung điểm của AC.

Câu 3

Tìm độ dài đoạn thẳng NQ trong Hình 4.

Tìm độ dài đoạn thẳng NQ trong Hình 4. (ảnh 1)

Lời giải

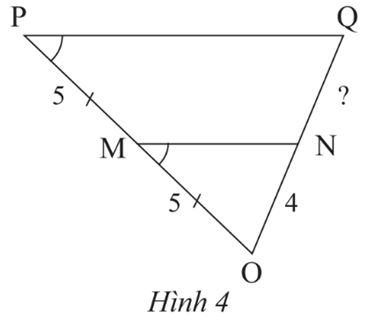
Ta có: OPQ^=OMN^ mà hai góc này ở vị trí đồng vị nên MN // PQ.

Xét tam giác OPQ ta có:

MN // PQ

M là trung điểm OP

Suy ra MN là đường trung bình tam giác OPQ.

Do đó là trung điểm OQ ⇒ NQ = ON = 4.

Câu 4

Trong Hình 5, chứng minh MN là đường trung bình của tam giác ABC.

Trong Hình 5, chứng minh MN là đường trung bình của tam giác ABC. (ảnh 1)

Lời giải

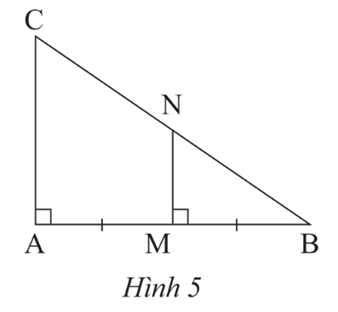
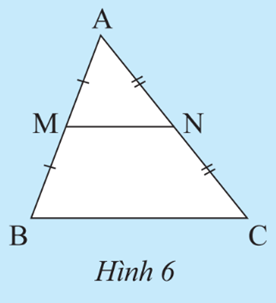
Ta có: MN ⊥ AB, AC ⊥ AB nên MN // AC.

Xét tam giác ABC có:

MN // AC

M là trung điểm AB

Suy ra MN là đường trung bình tam giác ABC.

Câu 5

Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC.

Tính các tỉ số AMAB, ANAC
Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC. Tính các tỉ số AM/AB AN/AC (ảnh 1)

Lời giải

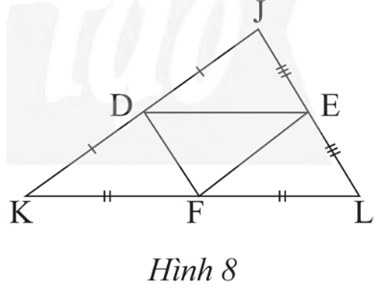
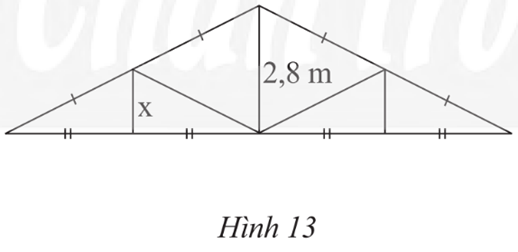
Vì M là trung điểm AB suy ra AMAB=12.

Tương tự, ANAC=12.

Câu 6

Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC.

Chứng minh MN // BC

Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC. Chứng minh MN // BC (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC.

Chứng minh MNBC=12
Cho M, N lần lượt là trung điểm của hai cạnh AB và AC của tam giác ABC. Chứng minh mn/bc = 1/2 (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Trong Hình 8, cho biết JK = 10 cm, DE = 6,5 cm, EL = 3,7 cm. Tính DJ, EF, DF, KL.

Trong Hình 8, cho biết JK = 10 cm, DE = 6,5 cm, EL = 3,7 cm. Tính DJ, EF, DF, KL. (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Hãy tính khoảng cách BC trong phần Hoạt động khởi động (trang 52).

Hãy tính khoảng cách BC trong phần Hoạt động khởi động (trang 52). (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Cho MN là đường trung bình của mỗi tam giác ABC trong Hình 9. Hãy tìm giá trị x trong mỗi hình.

Cho MN là đường trung bình của mỗi tam giác ABC trong Hình 9. Hãy tìm giá trị x trong mỗi hình. (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Tính độ dài đoạn PQ (Hình 10).

Tính độ dài đoạn PQ (Hình 10). (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Cho biết cạnh mỗi ô vuông bằng 1 cm. Tính độ dài các đoạn PQ, PR, RQ, AB, BC, CA trong Hình 11.

Cho biết cạnh mỗi ô vuông bằng 1 cm. Tính độ dài các đoạn PQ, PR, RQ, AB, BC, CA trong Hình 11. (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC (Hình 12).

a) Tam giác FBA và tam giác FCK có bằng nhau không? Vì sao?

Cho hình thang ABCD (AB // CD) có E và F lần lượt là trung điểm hai cạnh bên AD và BC. Gọi K là giao điểm của AF và DC (Hình 12). a) Tam giác FBA và tam giác FCK có bằng nhau không? Vì sao? (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

b) Chứng minh EF // CD // AB.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

c) Chứng minh  EF=AB+CD2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Một mái nhà được vẽ lại như Hình 13. Tính độ dài x trong hình mái nhà.

Một mái nhà được vẽ lại như Hình 13. Tính độ dài x trong hình mái nhà. (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Ảnh chụp từ Google Maps của một trường học được cho trong Hình 14. Hãy tính chiều dài cạnh DE, cho biết BC = 232 m và B, C lần lượt là trung điểm AD và AE.

Ảnh chụp từ Google Maps của một trường học được cho trong Hình 14. Hãy tính chiều dài cạnh DE, cho biết BC = 232 m và B, C lần lượt là trung điểm AD và AE. (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack72. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập

Đăng ký

Bạn đã có tài khoản?