Câu hỏi:
13/07/2024 725
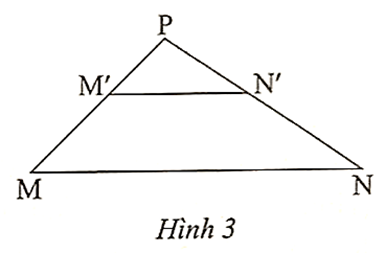
Cho tam giác MNP có có M'N' // MN (Hình 3). Đẳng thức nào sau đây sai?
A. \[\frac{{PM'}}{{PM}} = \frac{{PN}}{{PN'}}\];
B. \[\frac{{PM'}}{{PM}} = \frac{{PN'}}{{PN}}\];
C. \[\frac{{PM'}}{{M'M}} = \frac{{PN'}}{{N'N}}\];
D. \[\frac{{M'M}}{{PM}} = \frac{{N'N}}{{PN}}\].
Cho tam giác MNP có có M'N' // MN (Hình 3). Đẳng thức nào sau đây sai?
A. \[\frac{{PM'}}{{PM}} = \frac{{PN}}{{PN'}}\];
B. \[\frac{{PM'}}{{PM}} = \frac{{PN'}}{{PN}}\];
C. \[\frac{{PM'}}{{M'M}} = \frac{{PN'}}{{N'N}}\];
D. \[\frac{{M'M}}{{PM}} = \frac{{N'N}}{{PN}}\].
Câu hỏi trong đề: Giải SBT Toán 8 CTST Bài tập cuối chương 7 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
Xét ∆PMN có M'N' // MN nên theo định lí Thalès, ta có :
\[\frac{{PM'}}{{PM}} = \frac{{PN'}}{{PN}}\]; \[\frac{{PM'}}{{M'M}} = \frac{{PN'}}{{N'N}}\]; \[\frac{{M'M}}{{PM}} = \frac{{N'N}}{{PN}}\].
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: D
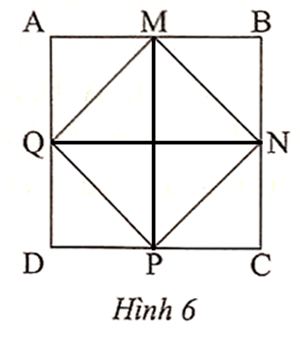
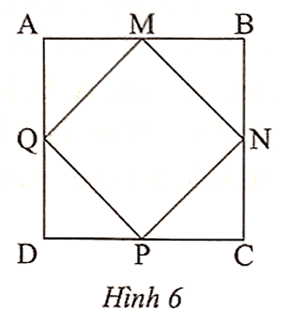
Vì ABCD là hình vuông và M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên
AM = MB = BN = NC = CP = PD = DQ = QA.
Suy ra AM2 + QA2 = MB2 + BN2 = NC2 + CP2 = PD2 + DQ2,
Khi đó MQ2 = MN2 = NP2 = PQ2 hay MQ = MN = NP = PQ,
Do đó tứ giác MNPQ là hình thoi (1)
• Vì AM = AQ nên ∆AMQ vuông cân tại A, suy ra \[\widehat {AMQ}\] = 45°.
• Vì BM = BN nên ∆BMN vuông cân tại B, suy ra \[\widehat {BMN}\] = 45°.
Mà \[\widehat {AMQ}\]+ \[\widehat {QMN}\] + \[\widehat {BMN}\] = 180°, suy ra \[\widehat {QMN}\] = 90° (2)
Từ (1) và (2) suy ra MNPQ là hình vuông.
SABCD = AB2 ; SMNPQ = MQ2
MQ2 = AM2 + QA2 = \[{\left( {\frac{1}{2}AB} \right)^2}\]+ \[{\left( {\frac{1}{2}AD} \right)^2}\]
= \[\frac{1}{4}\]AB2 + \[\frac{1}{4}\]AD2 = \[\frac{1}{4}\]AB2 + \[\frac{1}{4}\]AB2 = \[\frac{1}{2}\]AB2.
Do đó SMNPQ = \[\frac{1}{2}\]SABCD.
Lời giải
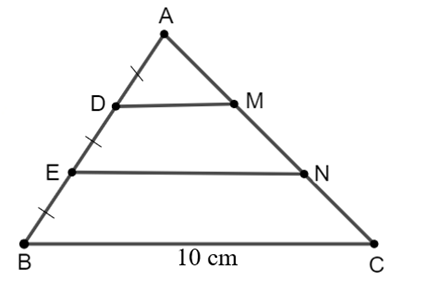
• Xét ∆ABC có DM // BC, theo hệ quả của định lí Thalès, ta có:
\[\frac{{DM}}{{BC}} = \frac{{AD}}{{AB}} = \frac{1}{3}\].
Suy ra DM = \[\frac{1}{3}\]BC = \[\frac{1}{3}\].10 = \[\frac{{10}}{3}\] (cm).
• Xét ∆ABC có EN // BC, theo hệ quả của định lí Thalès, ta có:
\[\frac{{EN}}{{BC}} = \frac{{AE}}{{AB}} = \frac{2}{3}\].
Suy ra EN = \[\frac{2}{3}\]BC = \[\frac{2}{3}\].10 = \[\frac{{20}}{3}\] (cm).
Vậy DM = \[\frac{{10}}{3}\] cm và EN = \[\frac{{20}}{3}\] cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận