Câu hỏi:
13/07/2024 10,821
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt phẳng (SAB) vuông góc với mặt đáy, tam giác SAB vuông cân tại S. Gọi M là trung điểm của AB. Chứng minh rằng:
a) SM ⊥ (ABCD);
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt phẳng (SAB) vuông góc với mặt đáy, tam giác SAB vuông cân tại S. Gọi M là trung điểm của AB. Chứng minh rằng:
a) SM ⊥ (ABCD);
Quảng cáo
Trả lời:
Giải bởi Vietjack
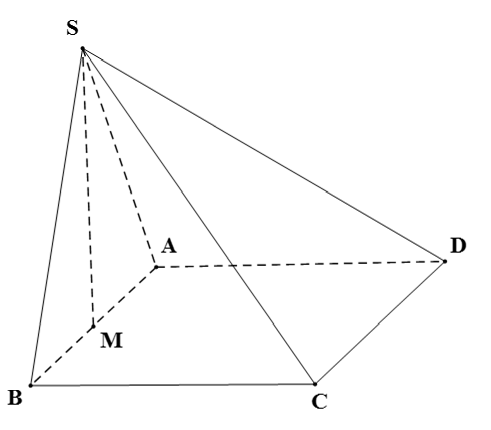
a) Xét tam giác SAB vuông cân tại S có: SM là đường trung tuyến (do M là trung điểm của AB) nên SM ⊥ AB.
Do A ∈ (SAB) ∩ (ABCD);
B ∈ (SAB) ∩ (ABCD).
Suy ra AB = (SAB) ∩ (ABCD).
Ta có: (SAB) ⊥ (ABCD);
SM ⊂ (SAB), SM ⊥ AB;
(SAB) ∩ (ABCD) = AB.
Từ đó, ta có SM ⊥ (ABCD).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
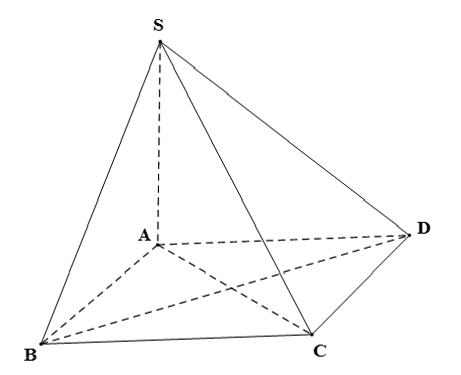
Ta có: SA ⊥ (ABCD) và BD ⊂ (ABCD) nên SA ⊥ BD.
Vì ABCD là hình thoi nên BD ⊥ AC.
Ta có: BD ⊥ SA, BD ⊥ AC và SA ∩ AC = A trong (SAC).
Suy ra BD ⊥ (SAC).
Mà BD ⊂ (SBD) nên (SAC) ⊥ (SBD).
Lời giải
Cho đường thẳng d không vuông góc với mặt phẳng (P). Ta cần chứng minh: tồn tại duy nhất mặt phẳng (Q) vuông góc với (P) và chứa d.
Chứng minh tính tồn tại mặt phẳng (Q):
· Xét trường hợp d cắt (P) tại A.
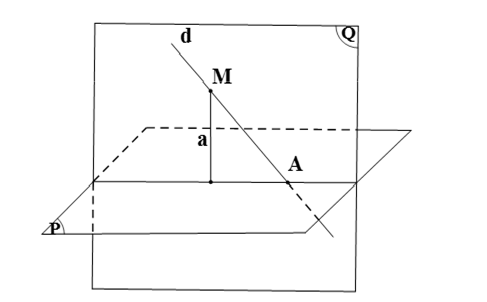
Lấy M ∈ d sao cho M ≠ A. Vẽ đường thẳng a đi qua M sao cho a ⊥ (P).
Suy ra d ∩ a = M.
Khi đó hai đường thẳng a và d xác định mặt phẳng (Q) hay mặt phẳng (Q) chứa hai đường thẳng a và d.
Vì a ⊥ (P), a ⊂ (Q) nên ta có (P) ⊥ (Q).
· Xét trường hợp d ⊂ (P) hoặc d // (P).
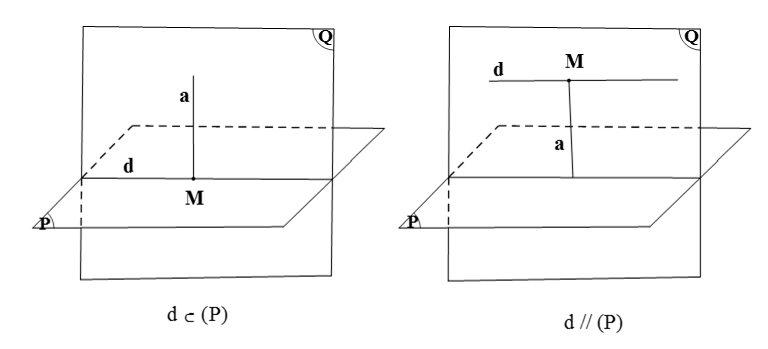
Lấy M ∈ d. Vẽ đường thẳng a đi qua M sao cho a ⊥ (P).
Suy ra d ∩ a = M.
Khi đó hai đường thẳng a và d xác định mặt phẳng (Q) hay mặt phẳng (Q) chứa hai đường thẳng a và d.
Vì a ⊥ (P), a ⊂ (Q) nên ta có (P) ⊥ (Q).
Chứng minh tính duy nhất mặt phẳng (Q):
Giả sử tồn tại mặt phẳng (Q’) khác (Q) sao cho d ⊂ (Q’) và (P) ⊥ (Q’).
Ta thấy: d = (Q’) ∩ (Q).
Mà (P) ⊥ (Q), (P) ⊥ (Q’) nên suy ra d ⊥ (P).
Mâu thuẫn với giả thiết d không vuông góc với (P).
Như vậy, tồn tại duy nhất mặt phẳng (Q) sao cho d ⊂ (Q) và (P) ⊥ (Q).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Lượng giác lớp 11 cơ bản, nâng cao có lời giải (P1)
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
10 Bài tập Biểu diễn góc lượng giác trên đường tròn lượng giác (có lời giải)
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
33 câu trắc nghiệm Toán 11 Kết nối tri thức Bài 29: Công thức cộng xác suất có đáp án
Nhắn tin Zalo