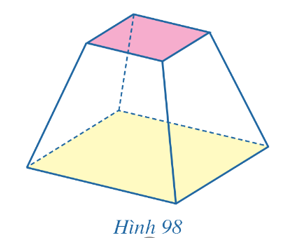
Cho hình chóp tam giác đều S.ABC. Chứng minh rằng các cạnh bên tạo với mặt phẳng chứa đáy các góc bằng nhau.
Cho hình chóp tam giác đều S.ABC. Chứng minh rằng các cạnh bên tạo với mặt phẳng chứa đáy các góc bằng nhau.
Quảng cáo
Trả lời:
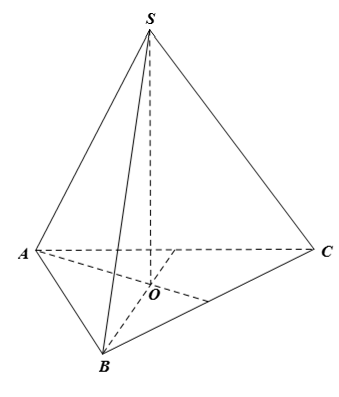
Do S.ABC là hình chóp tam giác đều nên SA = SB = SC (các cạnh bên bằng nhau).
Gọi O là chân đường cao của hình chóp tam giác đều S.ABC.
Do SO ⊥ (ABC) nên SO ⊥ OA, SO ⊥ OB, SO ⊥ OC.
Xét ∆SAO và ∆SBO có:
SO là cạnh chung;
SA = SB (chứng minh trên)
Do đó ∆SAO = ∆SBO (cạnh huyền – cạnh góc vuông)
Suy ra (hai góc tương ứng)
Chứng minh tương tự, ta cũng có∆SAO = ∆SCO nên
Từ đó ta có:
Vậy các cạnh bên tạo với mặt phẳng chứa đáy các góc bằng nhau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
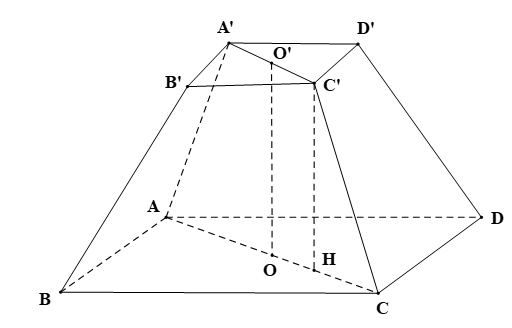
Mô hình hóa chân tháp của bài toán bằng khối chóp cụt tứ giác đều ABCD.A’B’C’D’, với O, O’ lần lượt là tâm của hai đáy ABCD và A’B’C’D’.
Như vậy ta có:
⦁ ABCD là hình vuông cạnh 5 có diện tích SABCD = 52 = 25;
⦁ A’B’C’D’ là hình vuông cạnh 2 có diện tích SA’B’C’D’ = 22 = 4;
⦁ Các cạnh bên A’A, B’B, C’C, D’D có độ dài bằng 3;
⦁ OO’ vuông góc với (ABCD) và (A’B’C’D’).
Do ABCD là hình vuông nên do đó tam giác ABC vuông tại B.
Áp dụng định lí Pythagore vào tam giác ABC vuông tại B có:
AC2 = AB2 + BC2 = 52 + 52 = 50.
Suy ra
Do đó (do O là tâm hình vuông ABCD).
Do A’B’C’D’ là hình vuông nên do đó tam giác A’B’C’ vuông tại B’.
Áp dụng định lí Pythagore trong tam giác A’B’C’ vuông tại B’ có:
A’C’2 = A’B’2 + B’C’2 = 22 + 22 = 8.
Suy ra
Do đó (do O’ là tâm hình vuông A’B’C’D’).
Dễ thấy: (ABCD) ∩ (A’C’CA) = AC;
(A’B’C’D’) ∩ (A’C’CA) = A’C’.
Mà (ABCD) // (A’B’C’D’).
Suy ra AC // A’C’ hay A’C’CA là hình thang.
Xét hình thang A’C’CA, kẻ C’H ⊥ AC (H ∈ AC).
Vì OO’ ⊥ (ABCD) và AC ⊂ (ABCD) nên OO’ ⊥ AC.
Do đó C’H // OO’ (cùng vuông góc với AC).
Mà O’C’ // OH (do A’C’ // AC)
Suy ra O’C’HO là hình bình hành.
Do đó: OO’ = C’H và
Suy ra
Áp dụng định lí Pythagore trong tam giác C’HC vuông tại H (do C’H ⊥ AC) có:
C’C2 = C’H2 + HC2
Suy ra
Do đó
Thể tích khối chóp cụt tứ giác đều ABCD.A’B’C’D’ với chiều cao và diện tích hai đáy SABCD = 25, SA’B’C’D’ = 4 là:
(m3).
Như vậy ta có thể tích của chân tháp đã cho bằng (m3).
Vì chân tháp được làm bằng bê tông tươi với giá tiền là 1 470 000 đồng/m3 nên số tiền để mua bê tông tươi làm chân tháp là:
(đồng).
Vậy số tiền để mua bê tông tươi làm chân tháp khoảng 40 538 432 đồng.
Lời giải
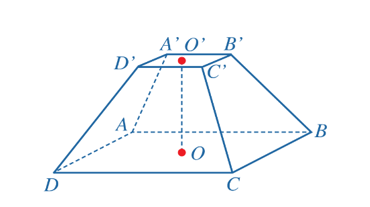
Một thùng đựng rác có dạng khối chóp cụt tứ giác đều nên ta có hai đáy là hình vuông.
Diện tích đáy lớn là S1 = 32 = 9 (dm2).
Diện tích đáy bé là S2 = 22 = 4 (dm2).
Vậy thể tích của thùng đựng rác có dạng khối chóp cụt tứ giác đều có chiều cao bằng 4 dm diện tích đáy hai đáy S1 = 9 dm2, S2 = 4 dm2 là:
(dm3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.