Cho tam giác ABC nhọn, các đường cao AD, BE, CF đồng quy tại H. Gọi M, N, P, Q lần lượt là hình chiếu của D trên AB, BE, CF, AC. Khẳng định nào sau đây sai?
Cho tam giác ABC nhọn, các đường cao AD, BE, CF đồng quy tại H. Gọi M, N, P, Q lần lượt là hình chiếu của D trên AB, BE, CF, AC. Khẳng định nào sau đây sai?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
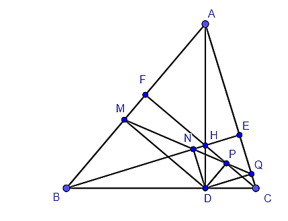
Ta có QD ⊥ AC, HE ⊥ AC (H ∈ BE) nên HE // QD hay BE // QD (H ∈ BE).
Xét tam giác ADQ có HE // DQ nên theo định lí Thalès ta có: \(\frac{{{\rm{AE}}}}{{{\rm{EQ}}}} = \frac{{{\rm{AH}}}}{{{\rm{HD}}}}\) (1).
Có HF ⊥ AB (H ∈ CF), DM ⊥ AB nên HF // DM hay CF // DM.
Xét tam giác AMD có HF // DM nên theo định lí Thalès ta có: \(\frac{{{\rm{AF}}}}{{{\rm{FM}}}} = \frac{{{\rm{AH}}}}{{{\rm{HD}}}}\) (2).
Từ (1) và (2) suy ra \(\frac{{{\rm{AE}}}}{{{\rm{EQ}}}} = \frac{{{\rm{AF}}}}{{{\rm{FM}}}}\).
Trong tam giác AMQ có \(\frac{{{\rm{AE}}}}{{{\rm{EQ}}}} = \frac{{{\rm{AF}}}}{{{\rm{FM}}}}\) nên EF // MQ (định lí Thaslès đảo) (*).
Xét tam giác BFC có CF // DM nên theo định lí Thalès ta có: \(\frac{{{\rm{BM}}}}{{{\rm{BF}}}} = \frac{{{\rm{BD}}}}{{{\rm{BC}}}}\) (3).
Có DN ⊥ BE, BE ⊥ EC (E ∈ AC) nên DN // CE.
Xét tam giác BEC có DN // CE nên theo định lí Thalès ta có: \(\frac{{{\rm{BN}}}}{{{\rm{BE}}}} = \frac{{{\rm{BD}}}}{{{\rm{BC}}}}\) (4).
Từ (3) và (4) suy ra \(\frac{{{\rm{BM}}}}{{{\rm{BF}}}} = \frac{{{\rm{BN}}}}{{{\rm{BE}}}}\).
Trong tam giác BEF có \(\frac{{{\rm{BM}}}}{{{\rm{BF}}}} = \frac{{{\rm{BN}}}}{{{\rm{BE}}}}\) nên MN // EF (định lí Thaslès đảo) (**).
Xét tam giác BEC có QD // BE nên theo định lí Thalès ta có: \(\frac{{{\rm{CQ}}}}{{{\rm{QE}}}} = \frac{{{\rm{CD}}}}{{{\rm{DB}}}}\) (5).
Có DP ⊥ CF, BF ⊥ CF (F ∈ AB) nên DP // BF.
Xét tam giác BFC có DP // BF nên theo định lí Thalès ta có: \(\frac{{{\rm{CP}}}}{{{\rm{PF}}}} = \frac{{{\rm{CD}}}}{{{\rm{DB}}}}\) (6).
Từ (5) và (6) suy ra \(\frac{{{\rm{CQ}}}}{{{\rm{QE}}}} = \frac{{{\rm{CP}}}}{{{\rm{PF}}}}\).
Trong tam giác CEF có \(\frac{{{\rm{CQ}}}}{{{\rm{QE}}}} = \frac{{{\rm{CP}}}}{{{\rm{PF}}}}\) nên PQ // EF (định lí Thaslès đảo)(***)
Từ (*), (**), (***) suy ra M, N, P, Q thẳng hàng.
Vậy A sai.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\frac{{{\rm{OF}}}}{{{\rm{FC}}}} = \frac{{{\rm{OA}}}}{{{\rm{OD}}}}\);
B. \(\frac{{{\rm{OF}}}}{{{\rm{OC}}}} = \frac{{{\rm{OD}}}}{{{\rm{OA}}}}\);
C. \(\frac{{{\rm{OE}}}}{{{\rm{OB}}}} = \frac{{{\rm{OD}}}}{{{\rm{OA}}}}\);
D. EF // BC.
Lời giải
Đáp án đúng là: A
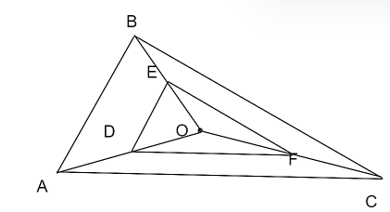
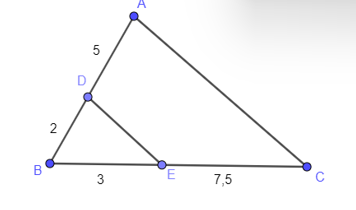
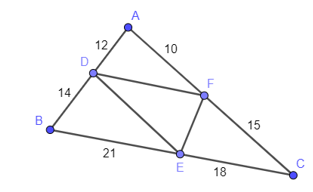
Xét tam giác OAB có DE // AB nên theo định lí Thalès ta có:
\(\frac{{{\rm{OE}}}}{{{\rm{OB}}}} = \frac{{{\rm{OD}}}}{{{\rm{OA}}}}\) (1)
Xét tam giác OAC có DF // AC nên theo định lí Thalès ta có:
\(\frac{{{\rm{OF}}}}{{{\rm{OC}}}} = \frac{{{\rm{OD}}}}{{{\rm{OA}}}}\) (2)
Từ (1) và (2) suy ra \(\frac{{{\rm{OE}}}}{{{\rm{OB}}}} = \frac{{{\rm{OF}}}}{{{\rm{OC}}}} = \frac{{{\rm{OD}}}}{{{\rm{OA}}}}\).
Trong tam giác OBC có \(\frac{{{\rm{OE}}}}{{{\rm{OB}}}} = \frac{{{\rm{OF}}}}{{{\rm{OC}}}}\) nên EF // BC (định lí Thalès đảo).
Vậy A sai.
Câu 2
Lời giải
Đáp án đúng là: C
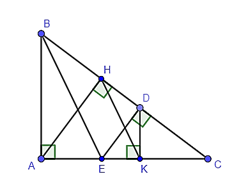
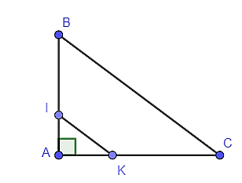
Có DE ⊥ DC nên DE ⊥ BC (D ∈ BC).
Vì AH ⊥ BC nên AH // DE.
Lại có DK ⊥ AC , AB ⊥ AC nên DK // AB.
Xét tam giác ABC có DK // AB nên theo định lí Thalès ta có:
\(\frac{{{\rm{CD}}}}{{{\rm{CB}}}} = \frac{{{\rm{CK}}}}{{{\rm{CA}}}}\)(1)
Xét tam giác AHC có DE // AH nên theo định lí Thalès ta có:
\(\frac{{{\rm{CD}}}}{{{\rm{CH}}}} = \frac{{{\rm{CE}}}}{{{\rm{CA}}}}\)(2)
Chia theo vế (1) cho (2) ta được:
\(\frac{{{\rm{CD}}}}{{{\rm{CB}}}}:\frac{{{\rm{CD}}}}{{{\rm{CH}}}} = \frac{{{\rm{CK}}}}{{{\rm{CA}}}}:\frac{{{\rm{CE}}}}{{{\rm{CA}}}}\)
Suy ra \(\frac{{{\rm{CH}}}}{{{\rm{CB}}}} = \frac{{{\rm{CK}}}}{{{\rm{CE}}}}\).
Trong tam giác CEB có \(\frac{{{\rm{CH}}}}{{{\rm{CB}}}} = \frac{{{\rm{CK}}}}{{{\rm{CE}}}}\) nên HK // BE (định lí Thaslès đảo).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập