Câu hỏi:

13/07/2024 3,608

Cho đường tròn (O; R) và dây cung AB = R. Điểm C thuộc cung lớn AB, C khác A và B. Tính số đo góc ACB.

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 9 Cánh diều Bài 4. Góc ở tâm. Góc nội tiếp có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Xét ∆AOB có: OA = OB = AB = R nên ∆AOB là tam giác đều, do đó $\hat{A O B} = 60 ° .$

Mà $\hat{A O B}$ là góc ở tâm và $\hat{A C B}$ là góc nội tiếp cùng chắn cung AB của đường tròn (O). Do đó $\hat{A C B} = \frac{1}{2} \cdot \hat{A O B} = \frac{1}{2} \cdot 60 ° = 30 ° .$

Vậy $\hat{A C B} = 30 ° .$

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Cường Chí

Làm câu 14 a,b

5 tháng trước
Trả lời

Xem thêm ...

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho đường tròn (O; R) và dây AB sao cho $\hat{A O B} = 90 ° .$ Giả sử M, N lần lượt là các điểm thuộc cung lớn AB và cung nhỏ AB (M, N khác A và B).

a) Tính độ dài đoạn thẳng AB theo R.

Xem đáp án

Lời giải

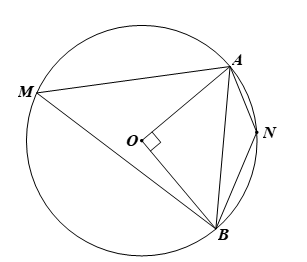
Cho đường tròn (O; R) và dây AB sao cho góc AOB=90 độ Giả sử M, N lần lượt là các điểm thuộc cung lớn AB (ảnh 1)

a) Xét đường tròn (O: R) có A, B thuộc đường tròn nên OA = OB = R.

Xét ∆AOB vuông tại O, theo định lí Pythagore, ta có:

AB² = OA² + OB² = R² + R² = 2R².

Do đó: $A B = \sqrt{2 R^{2}} = R \sqrt{2} .$

Câu 2

b) Tính số đo các góc ANB và AMB.

Xem đáp án

Lời giải

b) Xét đường tròn (O) có $\hat{A O B}$ là góc ở tâm chắn cung ANB nên $s đ \overset{⏜}{A N B} = \hat{A O B} = 90 ° .$

Ta có: $s đ \overset{⏜}{A M B} = 360 ° - s đ \overset{⏜}{A N B} = 360 ° - 90 ° = 270 ° .$

Vì $\hat{A N B}$ là góc nội tiếp chắn cung AMB nên $\hat{A N B} = \frac{1}{2} s đ \overset{⏜}{A M B} = \frac{1}{2} \cdot 270 ° = 135 ° .$

Vì $\hat{A M B}$ là góc nội tiếp chắn cung ANB nên $\hat{A M B} = \frac{1}{2} s đ \overset{⏜}{A N B} = \frac{1}{2} \cdot 90 ° = 45 ° .$

Câu 3

Biểu đồ hình quạt tròn ở Hình 64 mô tả các thành phần của một chai nước ép hoa quả (tính theo tỉ số phần trăm). Hãy cho biết các cung tương ứng với phần biểu diễn thành phần việt quất, táo, mật ong lần lượt có số đo là bao nhiêu độ.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Quan sát Hình 62, hãy cho biết:

a) 6 góc ở tâm có hai cạnh lần lượt chứa hai điểm trong bốn điểm A, B, C, D;

b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm A, B, C, D.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong Hình 63, cho biết AB = OA.

a) Tính số đo góc AOB.

b) Tính số đo cung nhỏ AB và cung lớn AB của (O).

c) Tính số đo góc MIN.

d) Tính số đo cung nhỏ MN và cung lớn MN của (I).

e) Tính số đo góc MKN.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hai đường tròn (O), (I) cắt nhau tại hai điểm A, B. Kẻ các đoạn thẳng AC, AD lần lượt là các đường kính của hai đường tròn (O), (I). Chứng minh ba điểm B, C, D thẳng hàng.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho đường tròn (O; R) và dây cung AB = R. Điểm C thuộc cung lớn AB, C khác A và B. Tính số đo góc ACB.

Cường Chí

Cho đường tròn (O; R) và dây AB sao cho AOB^=90°. Giả sử M, N lần lượt là các điểm thuộc cung lớn AB và cung nhỏ AB (M, N khác A và B). a) Tính độ dài đoạn thẳng AB theo R.

b) Tính số đo các góc ANB và AMB.

Quan sát Hình 62, hãy cho biết: a) 6 góc ở tâm có hai cạnh lần lượt chứa hai điểm trong bốn điểm A, B, C, D; b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm A, B, C, D.

Trong Hình 63, cho biết AB = OA. a) Tính số đo góc AOB. b) Tính số đo cung nhỏ AB và cung lớn AB của (O). c) Tính số đo góc MIN. d) Tính số đo cung nhỏ MN và cung lớn MN của (I). e) Tính số đo góc MKN.

Cho hai đường tròn (O), (I) cắt nhau tại hai điểm A, B. Kẻ các đoạn thẳng AC, AD lần lượt là các đường kính của hai đường tròn (O), (I). Chứng minh ba điểm B, C, D thẳng hàng.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho đường tròn (O; R) và dây AB sao cho $\hat{A O B} = 90 ° .$ Giả sử M, N lần lượt là các điểm thuộc cung lớn AB và cung nhỏ AB (M, N khác A và B).

a) Tính độ dài đoạn thẳng AB theo R.

Quan sát Hình 62, hãy cho biết:

a) 6 góc ở tâm có hai cạnh lần lượt chứa hai điểm trong bốn điểm A, B, C, D;

b) 4 góc nội tiếp có hai cạnh lần lượt chứa ba điểm trong bốn điểm A, B, C, D.

Trong Hình 63, cho biết AB = OA.

a) Tính số đo góc AOB.

b) Tính số đo cung nhỏ AB và cung lớn AB của (O).

c) Tính số đo góc MIN.

d) Tính số đo cung nhỏ MN và cung lớn MN của (I).

e) Tính số đo góc MKN.