Giải SBT Toán 9 Cánh Diều Bài 3. Tiếp tuyến của đường tròn

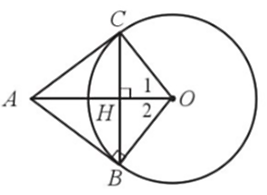
a) Xét ∆OBC có OB = OC nên ∆OBC cân tại O, suy ra đường cao OH của tam giác cũng đồng thời là đường phân giác của góc BOC, do đó $\widehat{O_1}=\widehat{O_2}.$

Do AB là tiếp tuyến của đường tròn (O) nên AB ⊥ OB hay $\widehat{ABO}=90°$

Xét ∆OAC và ∆OAB có:

OC = OB, $\widehat{O_1}=\widehat{O_2},$  cạnh OA chung

Do đó ∆OAC = ∆OAB (c.g.c).

Suy ra $\widehat{OCA}=\widehat{OBA}=90°$  hay AC vuông góc với OC tại C thuộc đường tròn (O).

Vậy AC là tiếp tuyến của đường tròn (O).

b) Xét ∆OAB vuông tại B, theo định lí Pythagore, ta có: OA² = AB² + OB²

Suy ra $AB=\sqrt{O{A}^2-O{B}^2}=\sqrt{{25}^2-{15}^2}=\sqrt{400}=20 \text{\hspace{0.17em}cm.}$

Xét ∆OBH và ∆OAB có: $\widehat{OHB}=\widehat{OBA}=90°$ và $\widehat{O}$  là góc chung

Do đó ∆OBH ᔕ ∆OAB (g.g)

Suy ra $\frac{BH}{AB}=\frac{OB}{OA}$  nên $BH=\frac{AB\cdot OB}{OA}=\frac{20\cdot 15}{25}=12 \text{cm}.$

Do ∆OBC cân tại O, suy ra đường cao OH của tam giác cũng đồng thời là đường trung tuyến hay H là trung điểm của BC, nên BC = 2BH = 2.12 = 24 cm.

Do ∆OAC = ∆OAB (chứng minh ở câu a) nên AC = AB = 20 cm.

Vậy tam giác ABC có AB = AC = 20 cm và BC = 24 cm.

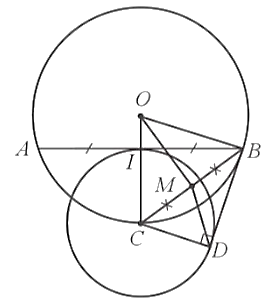
a) Gọi M là trung điểm của đoạn thẳng BC, khi đó $MB=MC=\frac{1}{2}BC.\left(1\right)$

Xét ∆OAB có OA = OB nên ∆OAB cân tại O, suy ra đường trung tuyến OI đồng thời là đường cao của tam giác, hay OC ⊥ AB tại I.

Ta có ∆BIC vuông tại I có IM là đường trung tuyến ứng với canh huyền BC nên $IM=\frac{1}{2}BC.\left(2\right)$

Ta có ∆BDC vuông tại D có DM là đường trung tuyến ứng với canh huyền BC nên $DM=\frac{1}{2}BC.\left(3\right)$

Từ (1), (2) và (3), suy ra $IM=DM=CM=BM=\frac{BC}{2}.$

Do đó bốn đỉnh của tứ giác BDCI cùng nằm trên đường tròn đường kính BC.

b) Đường tròn (C) có hai tiếp tuyến BI, BD cắt nhau tại B nên CB là tia phân giác của góc ICD, hay $\widehat{BCI}=\widehat{BCD}.$

Mặt khác, ∆OBC cân tại O (do OB = OC) nên $\widehat{OBC}=\widehat{OCB}$  hay  $\widehat{OBC}=\widehat{BCI}.$

Suy ra $\widehat{OBC}=\widehat{BCD},$  mà hai góc này ở vị trí so le trong nên OB // CD.

Lại có BD ⊥ CD nên BD ⊥ OB tại B, mà B nằm trên đường tròn (O)

Vậy BD là tiếp tuyến của đường tròn (O).

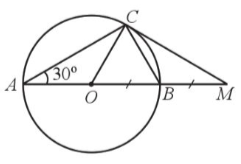
a) Ta có C nằm trên đường tròn (O) đường kính AB nên $OC=\frac{1}{2}AB$

Xét ∆ABC có CO là trung tuyến ứng với cạnh AB và $OC=\frac{1}{2}AB$  nên tam giác ABC vuông tại C, hay $\widehat{ACB}=90°$

Ta có ∆OAC cân tại O (do OA = OC = R) nên $\widehat{OCA}=\widehat{OAC}=30°$

Mà $\widehat{ACB}=\widehat{OCA}+\widehat{OCB}$  nên $\widehat{OCB}=\widehat{ACB}-\widehat{OCA}=90°-30°=60°$

Xét ∆OBC cân tại O (do OB = OC = R) có $\widehat{OCB}=60°$  nên ∆OBC là tam giác đều

Suy ra CB = OB.

Mà B là trung điểm của OM nên $OB=\frac{OM}{2}$  suy ra $CB=\frac{OM}{2}$

Xét ∆COM có CB là trung tuyến ứng với cạnh OM và $CB=\frac{OM}{2}$  nên tam giác COM vuông tại C, hay MC ⊥ OC tại C nằm trên đường tròn (O; R).

Vậy MC là tiếp tuyến của đường tròn (O).

b) Ta có B là trung điểm của OM nên OM = 2OB = 2R.

Xét ∆COM vuông tại C, theo định lí Pythagore, ta có: OM² = OC² + MC²

Suy ra $MC=\sqrt{O{M}^2-O{C}^2} =\sqrt{{\left(2R\right)}^2-R^2} =\sqrt{3R^2} =R\sqrt{3}$

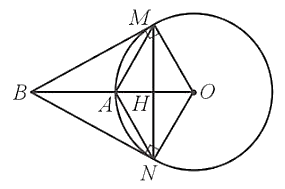
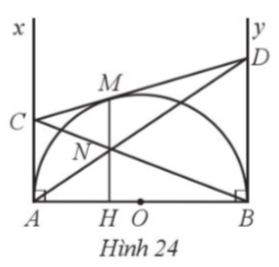
a) Do BM, BN là tiếp tuyến của đường tròn (O) cắt nhau tại B nên BM ⊥ OM và BO là tia phân giác của góc MBN.

Do A là trung điểm của OB, mà A thuộc đường tròn (O) nên OA = AB = R, hay OB = 2OA = 2R.

Vì tam giác MBO vuông tại M nên $\sin \widehat{OBM}=\frac{OM}{OB}=\frac{1}{2}$  Suy ra  $\widehat{OBM}=30°$

Do đó $\widehat{MBN}=2\widehat{OBM}=2\times 30°=60°$  (do BO là tia phân giác của góc MBN).

Xét ∆OBM vuông tại M, theo định lí Pythagore, ta có: OB² = OM² + BM²

Suy ra $BM=\sqrt{O{B}^2-O{M}^2}=\sqrt{{\left(2R\right)}^2-R^2} =\sqrt{3R^2} =R\sqrt{3}$

b) Xét tam giác OBM có:$\widehat{OBM}+\widehat{BOM}+\widehat{BMO}=180°$

Suy ra $\widehat{BOM}=180°-\widehat{OBM}-\widehat{BMO}=180°-30°-90°=60°$

Mà OM = OA = R, suy ra tam giác OAM là tam giác đều, nên OM = OA = AM. (1)

Tương tự, ta chứng minh được tam giác OAN là tam giác đều.

Suy ra OA = ON = AN. (2)

Từ (1), (2) suy ra AM = OM = ON = AN.

Do đó tứ giác AMON là hình thoi.

c) Do tứ giác AMON là hình thoi nên hai đường chéo MN và OA cắt nhau tại trung điểm H của mỗi đường, suy ra $OH=\frac{OA}{2}=\frac{R}{2}$

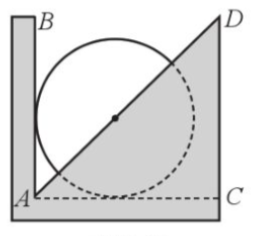
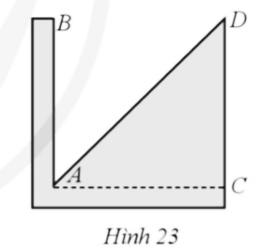
Để tìm tâm của một hình tròn, ta đặt hình tròn đó tiếp xúc với hai cạnh AB và AC. Vạch theo AD ta được một đường thẳng đi qua tâm của hình tròn. Xoay hình tròn và làm tương tự, ta được một đường thẳng nữa đi qua tâm của hình tròn. Giao điểm của hai đường vừa kẻ là tâm của hình tròn (hình vẽ).