Giải SBT Toán 9 Bài 3. Hình cầu có đáp án
30 người thi tuần này 4.6 248 lượt thi 10 câu hỏi
🔥 Đề thi HOT:
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
36 K lượt thi
4 câu hỏi
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
10.5 K lượt thi
5 câu hỏi
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
35.9 K lượt thi
3 câu hỏi
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 1: Đại số)
9.7 K lượt thi
188 câu hỏi
Bài tập theo tuần Toán 9 - Tuần 26
2.3 K lượt thi
36 câu hỏi
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
3.9 K lượt thi
12 câu hỏi
Nội dung liên quan:
Danh sách câu hỏi:
Lời giải
Gọi r là bán kính của hình cầu (r > 0).
Ta có diện tích hình tròn lớn của nó bằng πr2 và bằng 8π nên πr2 = 8π hay r2 = 8.
Vậy diện tích của mặt cầu đó là: 4πr2 = 4π.8 = 32π (cm2).
Lời giải
Gọi bán kính quả bida là r (mm) (r > 0).
Thể tích quả bida là \(\frac{4}{3}\pi {r^3}\) và bằng 36 000π mm3 nên ta có:
\(\frac{4}{3}\pi {r^3} = 36\,\,000\pi \)
Suy ra \[{r^3} = 36\,\,000:\frac{4}{3} = 27\,\,000\]
Do đó r = 30 mm.
Vậy đường kính quả bida đó là 2.30 = 60 mm = 6 cm.
Lời giải
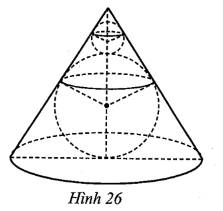
Từ 2R = l và 2l = 3r, suy ra \[R = \frac{l}{2},\,\,r = \frac{{2l}}{3}.\]
Diện tích mặt cầu (C) là: \(4\pi {R^2} = 4\pi \cdot {\left( {\frac{l}{2}} \right)^2} = 4\pi \cdot \frac{l}{4} = \pi {l^2}.\)
Diện tích toàn phần của hình nón (N) là:
\(\pi rl + \pi {r^2} = \pi \cdot \frac{{2l}}{3} \cdot l + \pi \cdot {\left( {\frac{{2l}}{3}} \right)^2} = \frac{2}{3}\pi {l^2} + \frac{4}{9}\pi {l^2} = \frac{{10\pi {l^2}}}{9}.\)
Do tổng diện tích mặt cầu (C) và diện tích toàn phần của hình nón (N) là 171π cm2 nên:
\(\pi {l^2} + \frac{{10\pi {l^2}}}{9} = 171\pi \) hay 19πl2 = 171π.9
Suy ra l2 = 81 nên l = 9 cm (do l > 0).
Khi đó, bán kính mặt cầu (C) là \[R = \frac{l}{2} = \frac{9}{2} = 4,5\] (cm).
Vậy diện tích của mặt cầu (C) là:
4πR2 = 4π.(4,5)2 = 81π ≈ 81.3,14 = 254,34 ≈ 254 (cm2).
Lời giải
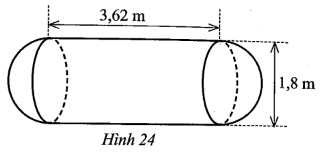
Ta có bán kính hình cầu và bán kính đáy hình trụ đều là: 1,8 : 2 = 0,9 (m).
Tổng thể tích của hai nửa hình cầu chính là thể tích của một hình cầu có cùng bán kính và bằng:
\(\frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \cdot {\left( {0,9} \right)^3} = 0,972\pi \) (m3).
Thể tích phần hình trụ là:
V = πR2h = π.(0,9)2.3,62 = 2,9322π (m3).
Thể tích của bồn chứa là:
0,972π + 2,9322π = 3,9042π ≈ 3,9042.3,14 ≈ 12,3 (m3).
Lời giải
Gọi bán kính đường tròn đáy của cái cốc là R (cm) (R > 0).
Thể tích viên bi có dạng hình cầu với bán kính là 3 cm là:
\(\frac{4}{3}\pi \cdot {3^3} = 36\pi \;\;({\rm{c}}{{\rm{m}}^3}).\)
Dễ thấy khi viên bi chìm xuống đáy cốc thì lượng nước trong cốc được dâng thêm bằng thể tích viên bi. Mặt khác, khi viên bi chìm xuống đáy cốc thì chiều cao mực nước dâng thêm 1,5 cm, do đó ta có πR2.1,5 = 36π.
Suy ra R2 = 24.
Thể tích của khối nước ban đầu trong cốc là:
πR2.7,2 = π.24.7,2 = 172,8π ≈ 172,8 . 3,14 ≈ 542,6 (cm3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo