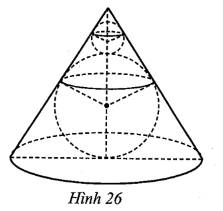
Người ta đổ đầy nước vào một bể hình lập phương cạnh 2a. Tiếp theo, người ta thả vào trong bể đó một vật thể có dạng hình cầu (đặc, không thấm nước) bán kính a như Hình 25. Hỏi lượng nước còn lại trong bể bằng bao nhiêu phần trăm lượng nước bị trào ra khỏi bể (làm tròn kết quả đến hàng phần mười)?
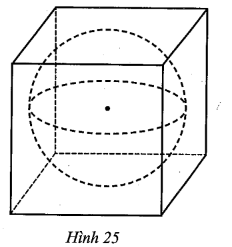
Người ta đổ đầy nước vào một bể hình lập phương cạnh 2a. Tiếp theo, người ta thả vào trong bể đó một vật thể có dạng hình cầu (đặc, không thấm nước) bán kính a như Hình 25. Hỏi lượng nước còn lại trong bể bằng bao nhiêu phần trăm lượng nước bị trào ra khỏi bể (làm tròn kết quả đến hàng phần mười)?

Câu hỏi trong đề: Giải SBT Toán 9 Bài 3. Hình cầu có đáp án !!
Quảng cáo
Trả lời:
Ta có lượng nước bị trào ra khỏi bể bằng thể tích hình cầu và bằng \(\frac{4}{3}\pi {a^3}.\)
Thể tích của bể nước có dạng hình lập phương đó là: (2a)3 = 8a3.
Do đó, lượng nước còn lại trong bể là:
\(8{a^3} - \frac{4}{3}\pi {a^3} = \frac{{\left( {24 - 4\pi } \right){a^3}}}{3}.\)
Ta có tỉ số phần trăm của lượng nước còn lại trong bể và lượng nước bị trào ra khỏi bể là:
\(\left[ {\frac{{\left( {24 - 4\pi } \right){a^3}}}{3}:\left( {\frac{4}{3}\pi {a^3}} \right)} \right] \cdot 100\% = \left[ {\frac{{\left( {24 - 4\pi } \right){a^3}}}{3} \cdot \frac{3}{{4\pi {a^3}}}} \right] \cdot 100\% \)
\( = \frac{{6 - \pi }}{\pi } \cdot 100\% \approx 91,1\% .\)
Vậy lượng nước còn lại trong bể bằng khoảng 91,1% lượng nước bị trào ra khỏi bể.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi bán kính đường tròn đáy của cái cốc là R (cm) (R > 0).
Thể tích viên bi có dạng hình cầu với bán kính là 3 cm là:
\(\frac{4}{3}\pi \cdot {3^3} = 36\pi \;\;({\rm{c}}{{\rm{m}}^3}).\)
Dễ thấy khi viên bi chìm xuống đáy cốc thì lượng nước trong cốc được dâng thêm bằng thể tích viên bi. Mặt khác, khi viên bi chìm xuống đáy cốc thì chiều cao mực nước dâng thêm 1,5 cm, do đó ta có πR2.1,5 = 36π.
Suy ra R2 = 24.
Thể tích của khối nước ban đầu trong cốc là:
πR2.7,2 = π.24.7,2 = 172,8π ≈ 172,8 . 3,14 ≈ 542,6 (cm3).
Lời giải
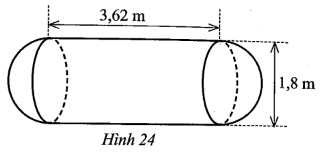
Ta có bán kính hình cầu và bán kính đáy hình trụ đều là: 1,8 : 2 = 0,9 (m).
Tổng thể tích của hai nửa hình cầu chính là thể tích của một hình cầu có cùng bán kính và bằng:
\(\frac{4}{3}\pi {R^3} = \frac{4}{3}\pi \cdot {\left( {0,9} \right)^3} = 0,972\pi \) (m3).
Thể tích phần hình trụ là:
V = πR2h = π.(0,9)2.3,62 = 2,9322π (m3).
Thể tích của bồn chứa là:
0,972π + 2,9322π = 3,9042π ≈ 3,9042.3,14 ≈ 12,3 (m3).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.