Giải SBT Toán 9 Bài tập cuối chương IX có đáp án
39 người thi tuần này 4.6 387 lượt thi 10 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
19 bài tập Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
Đáp án đúng là: B
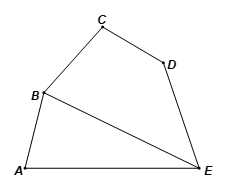
Tổng số đo tất cả các góc của ngũ giác ABCDE bằng tổng số đo các góc của tam giác ABE và tứ giác BCDE, và bằng: 180° + 360° = 540°.
Lời giải
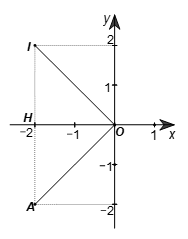
Gọi H là hình chiếu của A trên Ox. Ta có A(–2; –2) nên OH = AH = |–2| = 2.
Do đó ∆AOH vuông cân tại H, nên \(\widehat {AOH} = 45^\circ .\)
Xét ∆AOH vuông tại H, ta có: OA2 = OH2 + AH2 (định lí Pythagore).
Suy ra \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {{2^2} + {2^2}} = \sqrt 8 = 2\sqrt 2 .\)
Gọi I là điểm đối xứng với A qua Ox, do đó I(–2; 2). Ta cũng chứng minh được \(\widehat {HOI} = 45^\circ \) và \(OI = 2\sqrt 2 .\)
Như vậy, Phép quay thuận chiều 90° tâm O biến điểm A(–2; –2) thành điểm I(–2; 2).
Lời giải
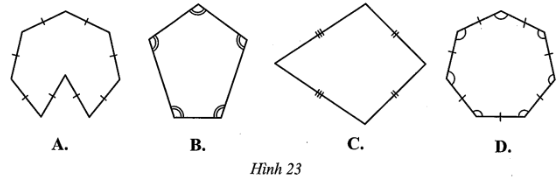
Đáp án đúng là: D
Hình A không phải đa giác lồi nên cũng không phải đa giác đều.
Hình B có các cạnh của đa giác không bằng nhau nên không phải đa giác đều.
Hình C có các góc của đa giác không bằng nhau nên không phải đa giác đều.
Hình D là đa giác lồi có các cạnh bằng nhau và các góc bằng nhau nên là đa giác lồi.
Lời giải
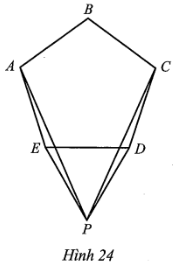
Tổng số đo tất cả các góc của ngũ giác ABCDE bằng tổng số đo các góc của tam giác ABE và tứ giác BCDE, và bằng: 180° + 360° = 540°.
Do ABCDE là ngũ giác đều suy ra các góc của nó đều bằng nhau và bằng \(\frac{{540^\circ }}{5} = 108^\circ .\)
Do PDE là tam giác đều nên PE = PD = DE và \[\widehat {PDE} = \widehat {PED} = \widehat {EPD} = 60^\circ .\]
Do đó: \(\widehat {AEP} = \widehat {AED} + \widehat {DEP} = 108^\circ + 60^\circ = 168^\circ ;\)
\(\widehat {CDP} = \widehat {CDE} + \widehat {EDP} = 108^\circ + 60^\circ = 168^\circ .\)
Do ABCDE là ngũ giác đều suy ra DE = EA = DC.
Do đó PE = PD = DE = EA = DC nên các tam giác EAP, DCP là các tam giác cân lần lượt tại các đỉnh E và D.
Suy ra: \(\widehat {EPA} = \frac{{180^\circ - \widehat {AEP}}}{2} = \frac{{180^\circ - 168^\circ }}{2} = 6^\circ ;\)
\(\widehat {DPC} = \frac{{180^\circ - \widehat {CDP}}}{2} = \frac{{180^\circ - 168^\circ }}{2} = 6^\circ .\)
Vì vậy ta có \(\widehat {APC} = \widehat {EPD} - \widehat {EPA} - \widehat {DPC} = 60^\circ - 6^\circ - 6^\circ = 48^\circ .\)
Lời giải
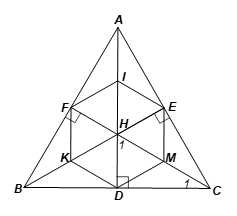
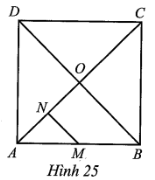
Vì ABC là tam giác đều và CF là đường cao nên CF cũng là đường phân giác của \(\widehat {ACB}.\) Suy ra \(\widehat {{C_1}} = \frac{1}{2}\widehat {ACB} = \frac{1}{2} \cdot 60^\circ = 30^\circ .\)
Tam giác HDC vuông tại D có
⦁ \[\widehat {{C_1}} + \widehat {{H_1}} = 90^\circ ,\] suy ra \[\widehat {{H_1}} = 90^\circ - \widehat {{C_1}} = 90^\circ - 30^\circ = 60^\circ ;\]
⦁ M là trung điểm của HC hay DM là đường trung tuyến ứng với cạnh huyền nên nên MD = MH = MC (cùng bằng một nửa cạnh huyền HC).
Do đó, tam giác DHM là tam giác đều.
Tương tự, ta cũng chứng minh được các tam giác HEM, HEI, HIF, HFK, HKD là các tam giác đều.
Từ đó suy ra lục giác DKFIEM có các góc đều bằng 2.60° = 120° và các cạnh đều bằng nhau, do đó lục giác DKFIEM là lục giác đều.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.