Câu hỏi:
25/08/2024 286
Trên mặt phẳng tọa độ Oxy cho hình vuông ABCD với A(0; 2), B(–2; 0), C(0; –2), D(2; 0). Phép quay thuận chiều 90° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Tính chu vi tứ giác A’B’C’D’.
Trên mặt phẳng tọa độ Oxy cho hình vuông ABCD với A(0; 2), B(–2; 0), C(0; –2), D(2; 0). Phép quay thuận chiều 90° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Tính chu vi tứ giác A’B’C’D’.
Câu hỏi trong đề: Giải SBT Toán 9 Bài tập cuối chương IX có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
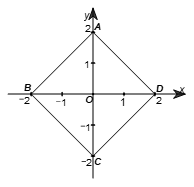
Do ABCD là hình vuông nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường.
Ta có A(0; 2), B(–2; 0), C(0; –2), D(2; 0) nên B, D cùng nằm trên Ox và A, C cùng nằm trên Oy.
Ta cũng suy ra được OA = OB = OC = OD hay O là tâm của hình vuông ABCD.
Xét ∆OAB vuông tại O, theo định lí Pythagore, ta có:
AB2 = OA2 + OB2 = 22 + 22 = 8.
Suy ra \(AB = \sqrt 8 = 2\sqrt 2 .\) Như vậy, hình vuông ABCD có cạnh bằng \(2\sqrt 2 .\)
Ta có phép quay thuận chiều 90° tâm O giữ nguyên hình vuông ABCD do đó chu vi tứ giác A’B’C’D’ bằng chu vi hình vuông ABCD và bằng \(4 \cdot 2\sqrt 2 = 8\sqrt 2 \) (đơn vị chiều dài).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
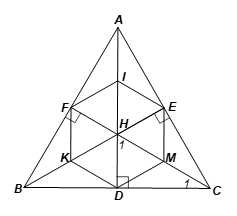
Vì ABC là tam giác đều và CF là đường cao nên CF cũng là đường phân giác của \(\widehat {ACB}.\) Suy ra \(\widehat {{C_1}} = \frac{1}{2}\widehat {ACB} = \frac{1}{2} \cdot 60^\circ = 30^\circ .\)
Tam giác HDC vuông tại D có
⦁ \[\widehat {{C_1}} + \widehat {{H_1}} = 90^\circ ,\] suy ra \[\widehat {{H_1}} = 90^\circ - \widehat {{C_1}} = 90^\circ - 30^\circ = 60^\circ ;\]
⦁ M là trung điểm của HC hay DM là đường trung tuyến ứng với cạnh huyền nên nên MD = MH = MC (cùng bằng một nửa cạnh huyền HC).
Do đó, tam giác DHM là tam giác đều.
Tương tự, ta cũng chứng minh được các tam giác HEM, HEI, HIF, HFK, HKD là các tam giác đều.
Từ đó suy ra lục giác DKFIEM có các góc đều bằng 2.60° = 120° và các cạnh đều bằng nhau, do đó lục giác DKFIEM là lục giác đều.
Lời giải
Đáp án đúng là: D
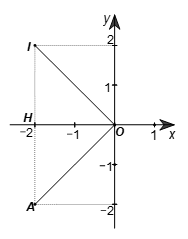
Gọi H là hình chiếu của A trên Ox. Ta có A(–2; –2) nên OH = AH = |–2| = 2.
Do đó ∆AOH vuông cân tại H, nên \(\widehat {AOH} = 45^\circ .\)
Xét ∆AOH vuông tại H, ta có: OA2 = OH2 + AH2 (định lí Pythagore).
Suy ra \(OA = \sqrt {O{H^2} + A{H^2}} = \sqrt {{2^2} + {2^2}} = \sqrt 8 = 2\sqrt 2 .\)
Gọi I là điểm đối xứng với A qua Ox, do đó I(–2; 2). Ta cũng chứng minh được \(\widehat {HOI} = 45^\circ \) và \(OI = 2\sqrt 2 .\)
Như vậy, Phép quay thuận chiều 90° tâm O biến điểm A(–2; –2) thành điểm I(–2; 2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo