Giải SBT Toán 9 Cánh diều Bài tập cuối chương VII có đáp án

Đáp án đúng là: D

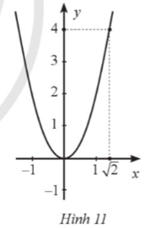
Giả sử hàm số cần tìm có dạng y = ax² (a ≠ 0).

Từ Hình 11, ta thấy đồ thị của hàm số đi qua điểm \(\left( {\sqrt 2 ;4} \right)\) nên ta có:

\(4 = a \cdot {\left( {\sqrt 2 } \right)^2},\) hay 2a = 4, suy ra a = 2.

Vậy hàm số cần tìm là y = 2x².

Đáp án đúng là: B

Phương trình 4x² – ax + 9 = 0 có ∆ = (‒a)² ‒ 4.4.9 = a² ‒ 144.

Để phương trình có nghiệm kép thì ∆ = 0, tức là a² ‒ 144 = 0, hay a² = 144, suy ra a = 12 hoặc a = ‒12.

Đồ thị hàm số y = (m + 2)x² (m ≠ –2) đi qua điểm A(–1; –2) nên thay x = ‒1 và y = ‒2 vào hàm số ta có:

–2 = (m + 2) .(–1)² hay m + 2 = –2, suy ra m = –4 (thỏa mãn m ≠ –2).

Do đó, hàm số là y = –2x².

a) Thay x = 3 vào hàm số y = –2x², ta có: y = –2.3² = –18.

Vậy giá trị của hàm số tại x = 3 là y = ‒18.

b) Xét điểm B(0,5; –0,25):

Thay x = 0,5 vào hàm số y = –2x², ta có y = –2.0,5² = –0,5 ≠ –0,25.

Do đó điểm B(0,5; –0,25) không thuộc đồ thị hàm số y = –2x².

c) Xét hàm số y = –2x².

• Ta có bảng giá trị của y tương ứng với giá trị của t như sau:

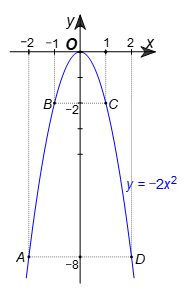
Do đó các điểm A(‒2; ‒8); B (‒1; ‒2); C(1; ‒2); D(2; ‒8) thuộc đồ thị hàm số y = –2x².

• Vẽ các điểm A(‒2; ‒8); B (‒1; ‒2); O(0; 0); C(1; ‒2); D(2; ‒8) thuộc đồ thị hàm số y = –2x² trong mặt phẳng tọa độ Oxy.

• Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số y = –2x² (hình vẽ).

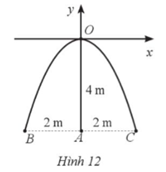
Từ Hình 12, ta thấy C(2; –4).

Đồ thị hàm số y = ax² đi qua C(2; –4) nên thay x = 2; y = ‒4 vào hàm số ta có:

–4 = a.2² hay 4a = –4, suy ra a = –1.

Do đó, y = –x².

Chiều cao của chiếc xe tải là 3m nên mái xe của chiếc xe tải còn cách vị trí cao nhất của cổng một khoảng là 4 – 3 = 1 (m).

Gọi K(0; –1) nằm trên trục Oy.

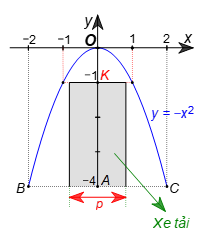
Thay y = –1 vào hàm số y = –x², ta được –1 = –x², hay x² = 1 nên x = –1 hoặc x = 1.

Để chiếc xe tải có chiều cao 3 m và chiều ngang p đi vào chính giữa cổng mà không chạm vào cổng thì p < 1 + 1 hay p < 2.

Dễ thấy, nếu p < 2 thì chiếc xe tải có chiều cao 3 m và chiều ngang p đi vào chính giữa cổng sẽ không chạm vào cổng.

Vậy p < 2.

a) \(\left( {\sqrt 2 - 1} \right){x^2} + x = 0\)

\[x\left[ {\left( {\sqrt 2 - 1} \right)x + 1} \right] = 0\]

x = 0 hoặc \[\left( {\sqrt 2 - 1} \right)x + 1 = 0\]

Từ \[\left( {\sqrt 2 - 1} \right)x + 1 = 0,\] suy ra \[x = \frac{{ - 1}}{{\sqrt 2 - 1}} = \frac{{ - \left( {\sqrt 2 + 1} \right)}}{{\left( {\sqrt 2 - 1} \right)\left( {\sqrt 2 + 1} \right)}} = \frac{{ - \sqrt 2 - 1}}{{2 - 1}} = - \sqrt 2 - 1.\]

Vậy phương trình đã cho có hai nghiệm phân biệt là \({x_1} = 0;\,\,{x_2} = - \sqrt 2 - 1.\)

b) 9x² – 17x + 4 = 0

Phương trình trên có ∆ = (‒17)² ‒ 4.9.4 = 145 > 0 nên phương trình có hai nghiệm phân biệt là:

\({x_1} = \frac{{17 - \sqrt {145} }}{{2 \cdot 9}} = \frac{{17 - \sqrt {145} }}{{18}};\)

\({x_2} = \frac{{17 + \sqrt {145} }}{{2 \cdot 9}} = \frac{{17 + \sqrt {145} }}{{18}}.\)

Vậy phương trình đã cho có hai nghiệm phân biệt là \({x_1} = \frac{{17 - \sqrt {145} }}{{18}};\,\,{x_2} = \frac{{17 + \sqrt {145} }}{{18}}.\)

c) –x² + 5,5x = 2x² – 3,3x + 4,84

–x² + 5,5x ‒ 2x² + 3,3x ‒ 4,84 = 0

‒3x² + 8,8x ‒ 4,84 = 0

Phương trình trên có ∆’ = 4,4² ‒ (‒3).(‒4,84) = 4,84 > 0 và \(\sqrt {\Delta '} = \sqrt {4,84} = 2,2.\)

Do đó phương trình có hai nghiệm phân biệt là

\[{x_1} = \frac{{ - 4,4 + 2,2}}{{ - 3}} = \frac{{ - 2,2}}{{ - 3}} = \frac{{22}}{{30}} = \frac{{11}}{{15}};\]

\[{x_2} = \frac{{ - 4,4 - 2,2}}{{ - 3}} = \frac{{ - 6,6}}{{ - 3}} = 2,2.\]

Vậy phương trình đã cho có hai nghiệm phân biệt là \[{x_1} = \frac{{11}}{{15}};\,\,{x_2} = 2,2.\]

d) \(\left( {\sqrt 3 - 5} \right){x^2} + 3x + 4 = \sqrt 3 {x^2} - 1.\)

\(\sqrt 3 {x^2} - 5{x^2} + 3x + 4 = \sqrt 3 {x^2} - 1\)

   5x² ‒ 3x ‒ 5 = 0.

Phương trình trên có ∆ = (‒3)² ‒ 4.5.(‒5) = 109 > 0, nên phương trình có hai nghiệm phân biệt là:

\({x_1} = \frac{{3 + \sqrt {109} }}{{2 \cdot 5}} = \frac{{3 + \sqrt {109} }}{{10}};\,\,{x_2} = \frac{{3 - \sqrt {109} }}{{2 \cdot 5}} = \frac{{3 - \sqrt {109} }}{{10}}.\)

Vậy phương trình đã cho có hai nghiệm phân biệt là \({x_1} = \frac{{3 + \sqrt {109} }}{{10}};\,\,{x_2} = \frac{{3 - \sqrt {109} }}{{10}}.\)

a) \( - 3{x^2} + 2\sqrt 5 x + 3 + 2\sqrt 5 = 0\)

Phương trình đã cho có các hệ số: a = ‒3; \[b = 2\sqrt 5 ;\,\,c = 3 + 2\sqrt 5 .\]

Ta thấy: \[a - b + c = - 3 - 2\sqrt 5 + 3 + 2\sqrt 5 = 0.\]

Do đó, phương trình có hai nghiệm \({x_1} = - 1;\,\,{x_2} = - \frac{{3 + 2\sqrt 5 }}{{ - 3}} = \frac{{3 + 2\sqrt 5 }}{3}.\)

Vậy phương trình đã cho có hai nghiệm phân biệt là \({x_1} = - 1;\,\,{x_2} = \frac{{3 + 2\sqrt 5 }}{3}.\)

b) \(\frac{1}{3}{x^2} - \frac{7}{{12}}x + \frac{1}{4} = 0\)

Phương trình đã cho có các hệ số: \[a = \frac{1}{3};\,\,b = - \frac{7}{{12}};\,\,c = \frac{1}{4}.\]

Ta thấy: \[a + b + c = \frac{1}{3} + \left( { - \frac{7}{{12}}} \right) + \frac{1}{4} = \frac{4}{{12}} - \frac{7}{{12}} + \frac{3}{{12}} = 0.\]

Do đó phương trình có hai nghiệm  \({x_1} = 1;\,\,{x_2} = \frac{{\frac{1}{4}}}{{\frac{1}{3}}} = \frac{3}{4}.\)

Vậy phương trình đã cho có hai nghiệm phân biệt là \({x_1} = 1;\,\,{x_2} = \frac{3}{4}.\)

c) 7x² + (3m – 1)x + 3m – 8 = 0.

Phương trình đã cho có các hệ số: a = 7; b = 3m ‒ 1; c = 3m ‒ 8.

Ta thấy: a ‒ b + c = 7 ‒ (3m – 1) + 3m ‒ 8 = 7 – 3m + 1 + 3m – 8 = 0.

Do đó, phương trình có hai nghiệm là \({x_1} = - 1;\,\,{x_2} = - \frac{{3m - 8}}{7} = \frac{{ - 3m + 8}}{7}.\)

Vậy phương trình đã cho có hai nghiệm phân biệt là \({x_1} = - 1,{x_2} = \frac{{ - 3m + 8}}{7}.\)