Câu hỏi:
25/08/2024 708
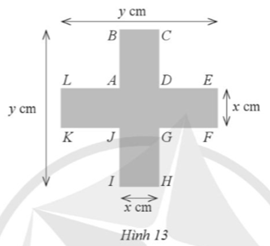
Một công ty sản xuất đường mía thấy rằng, khi giá bán một kilôgam đường mía là x nghìn đồng (x > 20) thì doanh thu từ bán đường mía được tính bởi công thức: R(x) = –550x2 + 22 000x (nghìn đồng).
a) Theo mô hình doanh thu đó, mức giá bán một kilôgam đường mía bằng bao nhiêu sẽ là quá cao dẫn đến việc doanh thu từ bán đường mía của công ty bằng 0 (tức là không có người mua)?
b) Tính giá bán mỗi kilôgam đường mía, biết doanh thu là 211 200 nghìn đồng.
Một công ty sản xuất đường mía thấy rằng, khi giá bán một kilôgam đường mía là x nghìn đồng (x > 20) thì doanh thu từ bán đường mía được tính bởi công thức: R(x) = –550x2 + 22 000x (nghìn đồng).
a) Theo mô hình doanh thu đó, mức giá bán một kilôgam đường mía bằng bao nhiêu sẽ là quá cao dẫn đến việc doanh thu từ bán đường mía của công ty bằng 0 (tức là không có người mua)?
b) Tính giá bán mỗi kilôgam đường mía, biết doanh thu là 211 200 nghìn đồng.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Doanh thu từ bán đường bằng 0 tức là –550x2 + 22 000x = 0.
Giải phương trình:
–550x2 + 22 000x = 0
x(‒550x + 22 000) = 0
x = 0 hoặc ‒550x + 22 000 = 0
x = 0 hoặc x = 40.
Ta thấy chỉ có giá trị x = 40 thoả mãn điều kiện x > 20.
Vậy mức giá bán một kilôgam đường mía bằng 40 nghìn đồng sẽ là quá cao dẫn đến việc doanh thu từ bán đường mía bằng 0 .
b) Doanh thu là 211 200 nghìn đồng nên ta có phương trình:
–550x2 + 22 000x = 211 200 hay x2 ‒ 40x + 384 = 0.
Phương trình trên có ∆’ = (‒20)2 ‒ 1.384 = 16 > 0 và \(\sqrt {\Delta '} = \sqrt {16} = 4.\)
Do đó phương trình có hai nghiệm phân biệt là
\[{x_1} = \frac{{20 + 4}}{1} = 26;\]
\[{x_2} = \frac{{20 - 4}}{1} = 16.\]
Ta thấy chỉ có giá trị x = 26 thoả mãn điều kiện x > 20.
Vậy giá bán mỗi kilôgam đường mía là 26 nghìn đồng.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
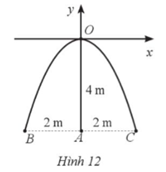
Từ Hình 12, ta thấy C(2; –4).
Đồ thị hàm số y = ax2 đi qua C(2; –4) nên thay x = 2; y = ‒4 vào hàm số ta có:
–4 = a.22 hay 4a = –4, suy ra a = –1.
Do đó, y = –x2.
Chiều cao của chiếc xe tải là 3m nên mái xe của chiếc xe tải còn cách vị trí cao nhất của cổng một khoảng là 4 – 3 = 1 (m).
Gọi K(0; –1) nằm trên trục Oy.
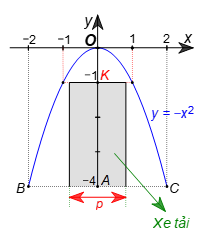
Thay y = –1 vào hàm số y = –x2, ta được –1 = –x2, hay x2 = 1 nên x = –1 hoặc x = 1.
Để chiếc xe tải có chiều cao 3 m và chiều ngang p đi vào chính giữa cổng mà không chạm vào cổng thì p < 1 + 1 hay p < 2.
Dễ thấy, nếu p < 2 thì chiếc xe tải có chiều cao 3 m và chiều ngang p đi vào chính giữa cổng sẽ không chạm vào cổng.
Vậy p < 2.
Lời giải
Xét phương trình: 2x2 + 2(m + 1)x – 3 = 0.
a) Phương trình đã cho có ∆’ = (m + 1)2 ‒ 2.(‒3) = (m + 1)2 + 6.
Với mọi m, ta có (m + 1)2 ≥ 0 nên (m + 1)2 + 6 ≥ 6 hay ∆’ > 0.
Vậy phương trình đó luôn có hai nghiệm phân biệt với mọi giá trị của m.
b) Theo định lí Viète, ta có:
\[{x_1} + {x_2} = \frac{{ - 2\left( {m + 1} \right)}}{2} = - m - 1\] và \[{x_1}{x_2} = \frac{{ - 3}}{2}.\]
Ta có: \[A = x_1^2 + x_2^2 + 3{x_1}{x_2}\]
= (x1 + x2)2 + x1x2
Thay x1 + x2 = – m – 1 và \[{x_1}{x_2} = \frac{{ - 3}}{2}\] vào biểu thức trên ta có:
\(A = {\left( { - m - 1} \right)^2} + \frac{{ - 3}}{2} = {\left( {m + 1} \right)^2} - \frac{3}{2}.\)
Với mọi m ta luôn có: (m + 1)2 ≥ 0 nên \({\left( {m + 1} \right)^2} - \frac{3}{2} \ge - \frac{3}{2}.\)
Khi đó, A có giá trị nhỏ nhất bằng \( - \frac{3}{2}\) khi m + 1 = 0 hay m = –1.
Vậy giá trị nhỏ nhất của biểu thức A là \( - \frac{3}{2}\) tại m = –1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận