Câu hỏi:
25/08/2024 635
Một biển báo giao thông có một phần dạng hình chữ thập với các kích thước x (cm), y (cm) và y = x + 25, AL = AB = CD = DE = FG = GH = IJ = JK như mô tả ở Hình 13.
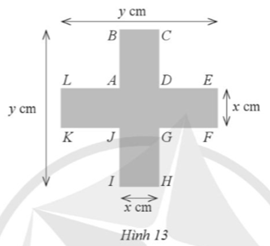
a) Tính diện tích phần hình chữ thập của biển báo giao thông đó theo x.
b) Tìm x nếu diện tích phần hình chữ thập của biển báo giao thông đó là 975 cm2.
Một biển báo giao thông có một phần dạng hình chữ thập với các kích thước x (cm), y (cm) và y = x + 25, AL = AB = CD = DE = FG = GH = IJ = JK như mô tả ở Hình 13.
a) Tính diện tích phần hình chữ thập của biển báo giao thông đó theo x.
b) Tìm x nếu diện tích phần hình chữ thập của biển báo giao thông đó là 975 cm2.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Độ dài AL là: \[\frac{{y - x}}{2} = \frac{{25 + x - x}}{2} = \frac{{25}}{2} = 12,5\,\,(cm).\]
Do AL = AB = CD = DE = FG = GH = IJ = JK nên diện tích phần không phải chữ thập (diện tích 4 hình vuông có cạnh bằng 12, 5 cm) là:
4.12,52 = 625 (cm2).
Diện tích biển báo giao thông có dạng hình vuông cạnh y (cm) là:
y2 = (x + 25)2 (cm2).
Diện tích phần hình chữ thập của biển báo giao thông đó là:
(x + 25)2 ‒ 625 = x2 + 50x ‒ 625 + 625 = x2 + 50x (cm2).
b) Theo bài, diện tích phần hình chữ thập của biển báo giao thông đó là 975 cm2 nên ta có phương trình: x2 + 50x = 975 hay x2 + 50x ‒ 975 = 0.
Phương trình trên có ∆’ = 252 ‒ 1.(‒975) = 1 600 > 0 và \(\sqrt {\Delta '} = \sqrt {1\,\,600} = 40.\)
Do đó phương trình có hai nghiệm phân biệt là:
\[{x_1} = \frac{{ - 25 + 40}}{1} = 15;\]
\[{x_2} = \frac{{ - 25 - 40}}{1} = - 65.\]
Ta thấy chỉ có giá trị x1 = 15 thỏa mãn điều kiện x > 0.
Vậy nếu diện tích phần hình chữ thập của biển báo giao thông đó là 975 cm2 thì x = 15 cm.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
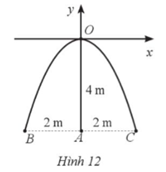
Từ Hình 12, ta thấy C(2; –4).
Đồ thị hàm số y = ax2 đi qua C(2; –4) nên thay x = 2; y = ‒4 vào hàm số ta có:
–4 = a.22 hay 4a = –4, suy ra a = –1.
Do đó, y = –x2.
Chiều cao của chiếc xe tải là 3m nên mái xe của chiếc xe tải còn cách vị trí cao nhất của cổng một khoảng là 4 – 3 = 1 (m).
Gọi K(0; –1) nằm trên trục Oy.
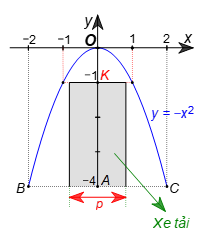
Thay y = –1 vào hàm số y = –x2, ta được –1 = –x2, hay x2 = 1 nên x = –1 hoặc x = 1.
Để chiếc xe tải có chiều cao 3 m và chiều ngang p đi vào chính giữa cổng mà không chạm vào cổng thì p < 1 + 1 hay p < 2.
Dễ thấy, nếu p < 2 thì chiếc xe tải có chiều cao 3 m và chiều ngang p đi vào chính giữa cổng sẽ không chạm vào cổng.
Vậy p < 2.
Lời giải
Xét phương trình: 2x2 + 2(m + 1)x – 3 = 0.
a) Phương trình đã cho có ∆’ = (m + 1)2 ‒ 2.(‒3) = (m + 1)2 + 6.
Với mọi m, ta có (m + 1)2 ≥ 0 nên (m + 1)2 + 6 ≥ 6 hay ∆’ > 0.
Vậy phương trình đó luôn có hai nghiệm phân biệt với mọi giá trị của m.
b) Theo định lí Viète, ta có:
\[{x_1} + {x_2} = \frac{{ - 2\left( {m + 1} \right)}}{2} = - m - 1\] và \[{x_1}{x_2} = \frac{{ - 3}}{2}.\]
Ta có: \[A = x_1^2 + x_2^2 + 3{x_1}{x_2}\]
= (x1 + x2)2 + x1x2
Thay x1 + x2 = – m – 1 và \[{x_1}{x_2} = \frac{{ - 3}}{2}\] vào biểu thức trên ta có:
\(A = {\left( { - m - 1} \right)^2} + \frac{{ - 3}}{2} = {\left( {m + 1} \right)^2} - \frac{3}{2}.\)
Với mọi m ta luôn có: (m + 1)2 ≥ 0 nên \({\left( {m + 1} \right)^2} - \frac{3}{2} \ge - \frac{3}{2}.\)
Khi đó, A có giá trị nhỏ nhất bằng \( - \frac{3}{2}\) khi m + 1 = 0 hay m = –1.
Vậy giá trị nhỏ nhất của biểu thức A là \( - \frac{3}{2}\) tại m = –1.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận