Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng y = ax2, gốc tọa độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét. Chiều cao OA, chiều rộng BC của cổng đều là 4 m (Hình 12). Giả sử một chiếc xe tải có chiều cao 3 m đi vào chính giữa cổng (qua điểm A). Chiều ngang p của chiếc xe tải phải thoả mãn điều kiện gì để có thể đi qua cổng mà không chạm vào cổng?
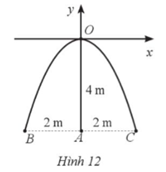
Một chiếc cổng hình parabol khi đưa vào hệ trục toạ độ Oxy có dạng y = ax2, gốc tọa độ O là vị trí cao nhất của cổng so với mặt đất, x và y được tính theo đơn vị mét. Chiều cao OA, chiều rộng BC của cổng đều là 4 m (Hình 12). Giả sử một chiếc xe tải có chiều cao 3 m đi vào chính giữa cổng (qua điểm A). Chiều ngang p của chiếc xe tải phải thoả mãn điều kiện gì để có thể đi qua cổng mà không chạm vào cổng?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Từ Hình 12, ta thấy C(2; –4).
Đồ thị hàm số y = ax2 đi qua C(2; –4) nên thay x = 2; y = ‒4 vào hàm số ta có:
–4 = a.22 hay 4a = –4, suy ra a = –1.
Do đó, y = –x2.
Chiều cao của chiếc xe tải là 3m nên mái xe của chiếc xe tải còn cách vị trí cao nhất của cổng một khoảng là 4 – 3 = 1 (m).
Gọi K(0; –1) nằm trên trục Oy.
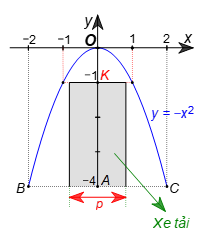
Thay y = –1 vào hàm số y = –x2, ta được –1 = –x2, hay x2 = 1 nên x = –1 hoặc x = 1.
Để chiếc xe tải có chiều cao 3 m và chiều ngang p đi vào chính giữa cổng mà không chạm vào cổng thì p < 1 + 1 hay p < 2.
Dễ thấy, nếu p < 2 thì chiếc xe tải có chiều cao 3 m và chiều ngang p đi vào chính giữa cổng sẽ không chạm vào cổng.
Vậy p < 2.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét phương trình: 2x2 + 2(m + 1)x – 3 = 0.
a) Phương trình đã cho có ∆’ = (m + 1)2 ‒ 2.(‒3) = (m + 1)2 + 6.
Với mọi m, ta có (m + 1)2 ≥ 0 nên (m + 1)2 + 6 ≥ 6 hay ∆’ > 0.
Vậy phương trình đó luôn có hai nghiệm phân biệt với mọi giá trị của m.
b) Theo định lí Viète, ta có:
\[{x_1} + {x_2} = \frac{{ - 2\left( {m + 1} \right)}}{2} = - m - 1\] và \[{x_1}{x_2} = \frac{{ - 3}}{2}.\]
Ta có: \[A = x_1^2 + x_2^2 + 3{x_1}{x_2}\]
= (x1 + x2)2 + x1x2
Thay x1 + x2 = – m – 1 và \[{x_1}{x_2} = \frac{{ - 3}}{2}\] vào biểu thức trên ta có:
\(A = {\left( { - m - 1} \right)^2} + \frac{{ - 3}}{2} = {\left( {m + 1} \right)^2} - \frac{3}{2}.\)
Với mọi m ta luôn có: (m + 1)2 ≥ 0 nên \({\left( {m + 1} \right)^2} - \frac{3}{2} \ge - \frac{3}{2}.\)
Khi đó, A có giá trị nhỏ nhất bằng \( - \frac{3}{2}\) khi m + 1 = 0 hay m = –1.
Vậy giá trị nhỏ nhất của biểu thức A là \( - \frac{3}{2}\) tại m = –1.
Lời giải
Đồ thị hàm số y = (m + 2)x2 (m ≠ –2) đi qua điểm A(–1; –2) nên thay x = ‒1 và y = ‒2 vào hàm số ta có:
–2 = (m + 2) .(–1)2 hay m + 2 = –2, suy ra m = –4 (thỏa mãn m ≠ –2).
Do đó, hàm số là y = –2x2.
a) Thay x = 3 vào hàm số y = –2x2, ta có: y = –2.32 = –18.
Vậy giá trị của hàm số tại x = 3 là y = ‒18.
b) Xét điểm B(0,5; –0,25):
Thay x = 0,5 vào hàm số y = –2x2, ta có y = –2.0,52 = –0,5 ≠ –0,25.
Do đó điểm B(0,5; –0,25) không thuộc đồ thị hàm số y = –2x2.
c) Xét hàm số y = –2x2.
• Ta có bảng giá trị của y tương ứng với giá trị của t như sau:
|
x |
‒2 |
‒1 |
1 |
2 |
|
y = –2x2 |
‒8 |
‒2 |
‒2 |
‒8 |
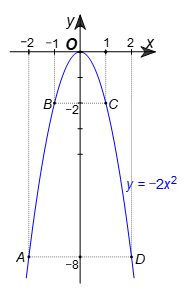
Do đó các điểm A(‒2; ‒8); B (‒1; ‒2); C(1; ‒2); D(2; ‒8) thuộc đồ thị hàm số y = –2x2.
• Vẽ các điểm A(‒2; ‒8); B (‒1; ‒2); O(0; 0); C(1; ‒2); D(2; ‒8) thuộc đồ thị hàm số y = –2x2 trong mặt phẳng tọa độ Oxy.
• Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số y = –2x2 (hình vẽ).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập