Giải SGK Toán 9 CD Bài 3. Ứng dụng của tỉ số lượng giác của góc nhọn có đáp án
43 người thi tuần này 4.6 1 K lượt thi 8 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
36 bài tập Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Ôn tập cuối chương 10 có đáp án
15 câu Trắc nghiệm Toán 9 Cánh diều Bài 3. Hình cầu có đáp án
6 bài tập Ứng dụng của mặt cầu trong thực tiễn (có lời giải)
3 bài tập Tính bán kính , diện tích, thể tích của mặt cầu (có lời giải)
20 bài tập Toán 9 Cánh diều Bài 2. Hình nón có đáp án
Danh sách câu hỏi:
Lời giải
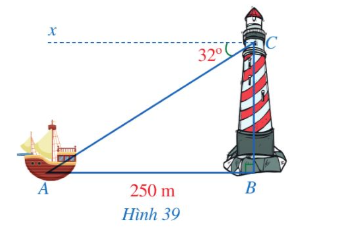
Ta có thể tính khoảng cách AB dựa vào độ cao BC và góc tạo bởi đường bay với phương nằm ngang.
Xét ∆ABC vuông tại C, ta có BC = AB.sinA, suy ra
Lời giải
⦁ Bài toán ở phần mở đầu:
Xét ∆ABC vuông tại C, ta có:
BC = AB.sinA, suy ra
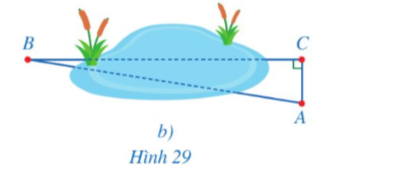
⦁ Hình 29b:
Xét ∆ABC vuông tại C, ta có:
AC = AB.cosA, suy ra
Lời giải
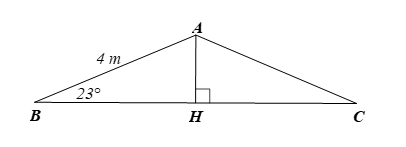
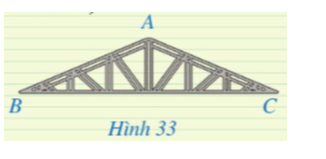
Kẻ AH ⊥ BC.
Vì ∆ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến, do đó H là trung điểm của BC, nên BC = 2BH.
Xét ∆ABH vuông tại H, ta có: BH = AB.cosB = 4.cos23° ≈ 3,7 (m).
Do đó BC = 2BH ≈ 2.3,7 = 7,4 (m).
Vậy BC ≈ 7,4 m.
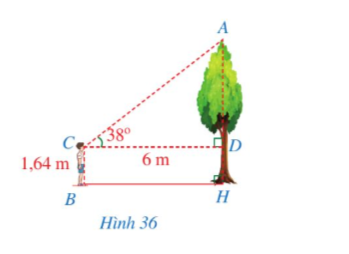
Lời giải
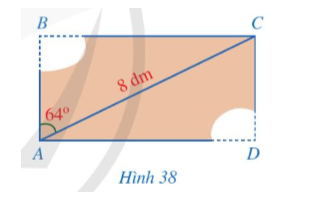
Xét ∆ACD vuông tại D, ta có:
Ta có AG = AD + DH ≈ 4,69 + 1,64 = 6,33 (m).
Vậy chiều cao AH của cây khoảng 6,33 m.
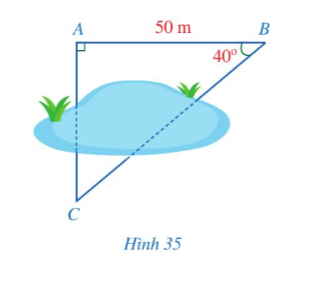
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.