Câu hỏi:

13/07/2024 2,567

Có thể tính phương sai và độ lệch chuẩn của mẫu số liệu ở biểu đồ trên không?

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 12 CTST Bài 2. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm có đáp án !!

Giao bài

Quảng cáo

Trả lời:

Giải bởi Vietjack

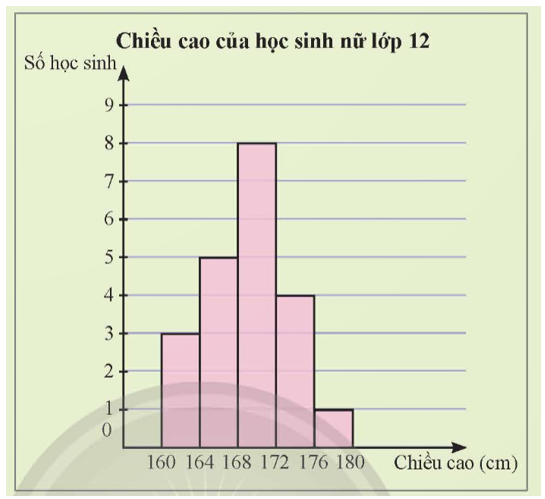
Sau bài học này, ta có thể tính được phương sai và độ lệch chuẩn của mẫu số liệu ở biểu đồ trên như sau:

Từ biểu đồ, ta lập được bảng tần số ghép nhóm sau:

Chiều cao (cm)	[160; 164)	[164; 168)	[168; 172)	[172; 176)	[176; 180)
Số học sinh	3	5	8	4	1

Ta có bảng thống kê chiều cao của các học sinh nữ lớp 12 theo giá trị đại diện:

Chiều cao

đại diện (cm)

162

166

170

174

178

Tần số

Cỡ mẫu n = 3 + 5 + 8 + 4 + 1 = 21.

Số trung bình của mẫu số liệu ghép nhóm là: $\bar{x} = \frac{3 \cdot 162 + 5 \cdot 166 + 8 \cdot 170 + 4 \cdot 174 + 1 \cdot 178}{21} = \frac{3550}{21}$ .

Phương sai của mẫu số liệu ghép nhóm là: $S^{2} = \frac{1}{21} [3 {(162 - \frac{3550}{21})}^{2} + 5 {(166 - \frac{3550}{21})}^{2} + ... + 1 {(178 - \frac{3550}{21})}^{2}]$

$= \frac{8000}{441}$ ≈ 18,14.

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $S = \sqrt{S^{2}} = \sqrt{\frac{8000}{441}} = \frac{40 \sqrt{5}}{21} \approx 4,26$ .

Đang tải chế độ Học...

Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay

ĐẶC QUYỀN VIP

Đăng ký VIP để học và luyện thi không giới hạn

Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.

Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
Đăng ký ngay

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Bảng dưới đây thống kê cự li ném tạ của một vận động viên.

Cự li (m)

[19; 19,5)

[19,5; 20)

[20; 20,5)

[20,5; 21)

[21; 21,5)

Tần số

13

45

24

12

6

Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.

Xem đáp án

Lời giải

Ta có bảng sau:

Cự li (m)

[19; 19,5)

[19,5; 20)

[20; 20,5)

[20,5; 21)

[21; 21,5)

Giá trị

đại diện

19,25

19,75

20,25

20,75

21,25

Tần số

Cỡ mẫu là n = 13 + 45 + 24 + 12 + 6 = 100.

Số trung bình của mẫu số liệu ghép nhóm là: $\bar{x} = \frac{13 \cdot 19,25 + 45 \cdot 19,75 + 24 \cdot 20,25 + 12 \cdot 20,75 + 6 \cdot 21,25}{100} = 20,015$ .

Phương sai của mẫu số liệu ghép nhóm là:

$S^{2} = \frac{1}{100}$ [13 ∙ (19,25)² + 45 ∙ (19,75)² + 24 ∙ (20,25)²

+ 12 ∙ (20,75)² + 6 ∙ (21,25)²] – (20,015)² ≈ 0,277.

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $S = \sqrt{S^{2}} \approx \sqrt{0,277} \approx 0,526$ .

Câu 2

Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết của pin một số máy vi tính cùng loại được mô tả bằng biểu đồ bên.

a) Hãy cho biết có bao nhiêu máy vi tính có thời gian sử dụng pin từ 7,2 đến dưới 7,4 giờ?

b) Hãy xác định số trung bình và độ lệch chuẩn của thời gian sử dụng pin.

Xem đáp án

Lời giải

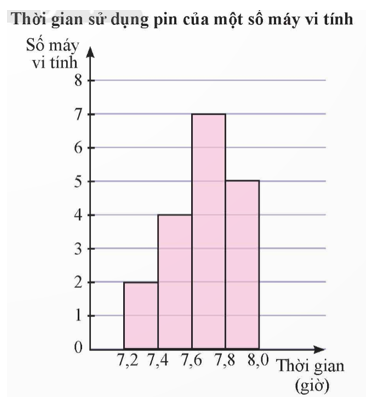
a) Từ biểu đồ ta thấy có 2 máy vi tính có thời gian sử dụng pin từ 7,2 đến dưới 7,4 giờ.

b) Từ biểu đồ, ta có bảng thống kê sau:

Thời gian (giờ)	[7,2; 7,4)	[7,4; 7,6)	[7,6; 7,8)	[7,8; 8,0)
Giá trị đại diện	7,3	7,5	7,7	7,9
Số máy vi tính	2	4	7	5

Cỡ mẫu là n = 2 + 4 + 7 + 5 = 18.

Số trung bình của mẫu số liệu ghép nhóm là: $\bar{x} = \frac{2 \cdot 7,3 + 4 \cdot 7,5 + 7 \cdot 7,7 + 5 \cdot 7,9}{18} \approx 7,667$ .

Phương sai của mẫu số liệu ghép nhóm là:

$S^{2} = \frac{1}{18}$ [2 ∙ (7,3)² + 4 ∙ (7,5)² + 7 ∙ (7,7)² + 5 ∙ (7,9)²] – (7,667)² ≈ 0,032.

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: $S = \sqrt{S^{2}} \approx \sqrt{0,032} \approx 0,179$ .

Câu 3