Cho hình chóp $S.ABCD$, gọi $O$ là giao điểm của hai đường chéo $BD$ và $AC.$ Phát biểu nào dưới đây đúng?

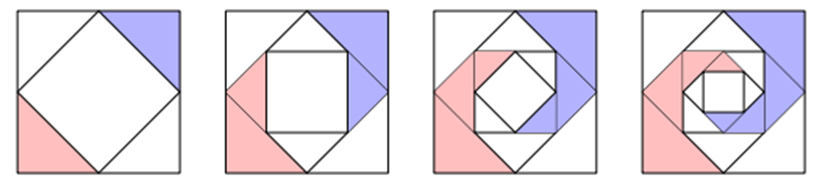
Theo quy luật trang trí một hình vuông trên thì ta có các tam giác được tô màu sẽ là tam giác vuông cân.

Gọi ${u_n}$ là diện tích của hai tam giác được tô màu sau lần vẽ thứ $n$, với $n \in {\mathbb{N}^*}.$

Độ dài cạnh góc vuông của hai tam giác vuông cân được tô màu theo lần vẽ đầu tiên là $\frac{4}{2} = 2\,\,\,\left( {\text{m}} \right).$ Khi đó diện tích của hai tam giác được tô màu sau lần vẽ đầu tiên là

${u_1} = 2\left( {\frac{1}{2}.2.2} \right) = 4$ $\left( {{{\text{m}}^{\text{2}}}} \right){\text{.}}$

Độ dài cạnh góc vuông của hai tam giác vuông cân được tô màu theo lần vẽ thứ hai là $\frac{1}{2}.\sqrt {{2^2} + {2^2}} \, = \sqrt 2 \,\,\left( {\text{m}} \right).$ Khi đó diện tích của hai tam giác được tô màu sau lần vẽ thứ hai là

 ${u_2} = 2\left( {\frac{1}{2}.\sqrt 2 .\sqrt 2 } \right) = 4.\frac{1}{2}$ $\left( {{{\text{m}}^{\text{2}}}} \right){\text{.}}$

Độ dài cạnh góc vuông của hai tam giác vuông cân được tô màu theo lần vẽ thứ ba là\[\frac{1}{2}.\sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} = 1\,\,\left( {\text{m}} \right).\] Khi đó diện tích của hai tam giác được tô màu sau lần vẽ thứ ba là

${u_3} = 2\left( {\frac{1}{2}.1.1} \right) = 4.{\left( {\frac{1}{2}} \right)^2}$ $\left( {{{\text{m}}^{\text{2}}}} \right){\text{.}}$

Khi đó, dãy số $\left( {{u_n}} \right)$ là một cấp số nhân với số hạng đầu ${u_1} = 4$ và công bội $q = \frac{1}{2}.$

Ta có công thức số hạng tổng quát ${u_n} = 4.{\left( {\frac{1}{2}} \right)^{n - 1}}$ $\left( {{{\text{m}}^{\text{2}}}} \right){\text{.}}$

Tổng diện tích của các tam giác được tô màu sau lần vẽ thứ 10 là:

${S_{10}} = \frac{{4\left[ {1 - {{\left( {\frac{1}{2}} \right)}^{10}}} \right]}}{{1 - \frac{1}{2}}} = \frac{{1\,\,023}}{{128}}$ $\left( {{{\text{m}}^{\text{2}}}} \right){\text{.}}$

Vậy số tiền nước sơn là $\frac{{1\,\,023}}{{128}}.80\,\,000 = 639\,\,375$ đồng.