Câu hỏi:
12/07/2024 201
Cho hình chóp $S.ABC$, gọi $M,\,\,P$ và $I$ lần lượt là trung điểm của $AB,\,\,SC$ và $SB$. Mặt phẳng $(\alpha )$ qua $MP$ và song song với $AC$ và cắt các cạnh $SA,\,\,BC$ tại $N,\,\,Q.$
a) Chứng minh đường thẳng $BC$ song sòng với mặt phẳng $(IMP)$.
b) Xác định thiết diện của $(\alpha )$ và hình chóp. Thiết diện này là hình gì?
c) Tìm giao điểm của đường thẳng $CN$ và mặt phẳng $(SMQ)$.
Cho hình chóp $S.ABC$, gọi $M,\,\,P$ và $I$ lần lượt là trung điểm của $AB,\,\,SC$ và $SB$. Mặt phẳng $(\alpha )$ qua $MP$ và song song với $AC$ và cắt các cạnh $SA,\,\,BC$ tại $N,\,\,Q.$
a) Chứng minh đường thẳng $BC$ song sòng với mặt phẳng $(IMP)$.
b) Xác định thiết diện của $(\alpha )$ và hình chóp. Thiết diện này là hình gì?
c) Tìm giao điểm của đường thẳng $CN$ và mặt phẳng $(SMQ)$.
Câu hỏi trong đề:
Đề kiểm tra Giữa kì 1 Toán 11 CTST có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
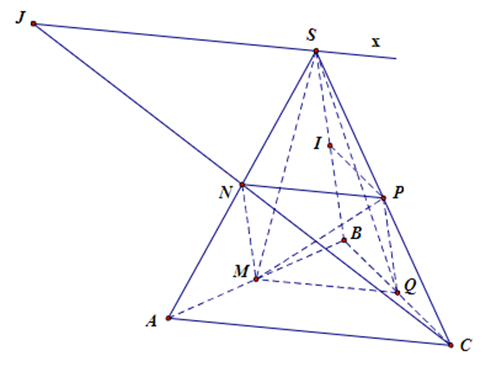
a) Ta có $IP$ là đường trung bình của tam giác $SBC$ nên $IP\,{\text{//}}\,BC$.
Mà $IP \subset (IMP)$ nên \[BC\,\,{\text{//}}\,(IMP)\].
b) Ta có $\left\{ \begin{gathered}
M \in (\alpha ) \cap (ABC) \hfill \\
(ABC) \supset AC\,{\text{//}}\,(\alpha ) \hfill \\
\end{gathered} \right.$.
Khi đó $(\alpha ) \cap (ABC) = MQ\,{\text{//}}\,AC,\,\,Q \in BC$.
Mặt khác c$\left\{ \begin{gathered}
P \in (\alpha ) \cap (SAC) \hfill \\
(SAC) \supset AC\,{\text{//}}\,(\alpha ) \hfill \\
\end{gathered} \right.$
Suy ra $(\alpha ) \cap (SAC) = PN\,{\text{//}}\,AC,\,\,N \in SA$.
Vậy thiết diện cần tìm là hình bình hành $MNPQ$.
c) Chọn mặt phẳng $(SAC)$ chứa $NC$. Tìm giao tuyến của $(SAC)$ và $(SMQ)$:
Ta có $\left\{ \begin{gathered}
S \in (SAC) \cap (SMQ) \hfill \\
AC\,{\text{//}}\,MQ,\,\,AC \subset (SAC),\,\,MQ \subset (SMQ) \hfill \\
\end{gathered} \right.$.
Do đó \[(SAC) \cap (SMQ) = Sx\,{\text{//}}\,AC\,{\text{//}}\,MQ\].
Trong mặt phẳng $(SAC)$, gọi $J = CN \cap Sx$.
Ta có $\left\{ \begin{gathered}
J \in CN \hfill \\
J \in Sx \subset (SMQ) \hfill \\
\end{gathered} \right. \Rightarrow J = CN \cap (SMQ)$.
Vậy $J$ là giao điểm của đường thẳng $CN$ và mặt phẳng $(SMQ)$.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng tọa độ $Oxy,$ trên đường tròn lượng giác như hình vẽ bên dưới. Điểm nào trong bốn đáp án A, B, C, D biểu diễn cho góc lượng giác có số đo bằng $60^\circ ?$
Trong mặt phẳng tọa độ $Oxy,$ trên đường tròn lượng giác như hình vẽ bên dưới. Điểm nào trong bốn đáp án A, B, C, D biểu diễn cho góc lượng giác có số đo bằng $60^\circ ?$
Xem đáp án »
25/04/2024
4,756
Câu 2:
Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} \ne 0$ và $q \ne 0$. Đẳng thức nào sau đây là đúng?
Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} \ne 0$ và $q \ne 0$. Đẳng thức nào sau đây là đúng?
Xem đáp án »
25/04/2024
4,224
Câu 3:
Cho dãy số $\left( {{u_n}} \right)$, với ${u_n} = {\left( {\frac{{n - 1}}{{n + 1}}} \right)^{2n + 3}}$. Tìm số hạng ${u_{n + 1}}$.
Cho dãy số $\left( {{u_n}} \right)$, với ${u_n} = {\left( {\frac{{n - 1}}{{n + 1}}} \right)^{2n + 3}}$. Tìm số hạng ${u_{n + 1}}$.
Xem đáp án »
25/04/2024
3,586
Câu 4:
Cho $\alpha $ thuộc góc phần phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?
Cho $\alpha $ thuộc góc phần phần tư thứ ba của đường tròn lượng giác. Khẳng định nào sau đây là sai?
Xem đáp án »
25/04/2024
2,549
Câu 5:
Cho góc lượng giác $\left( {Oa,Ob} \right)$ có số đo là $50^\circ .$ Hỏi số đo của góc luọng giác nào trong bốn đáp án A, B, C, D bên dưới cũng có tia đầu là $Oa$ và tia cuối là $Ob?$
Cho góc lượng giác $\left( {Oa,Ob} \right)$ có số đo là $50^\circ .$ Hỏi số đo của góc luọng giác nào trong bốn đáp án A, B, C, D bên dưới cũng có tia đầu là $Oa$ và tia cuối là $Ob?$
Xem đáp án »
11/07/2024
1,966
Câu 6:
Tất cả nghiệm của phương trình $\cot 2x = \cot \frac{\pi }{3}$ là
Xem đáp án »
25/04/2024
1,732
về câu hỏi!