Cho hai hình vuông ABCD và MNDQ lần lượt có cạnh là 12 cm và 10 cm. Nói Q và B, gọi P là giao điểm của QB và AD. Tính diện tích hình tô đậm.
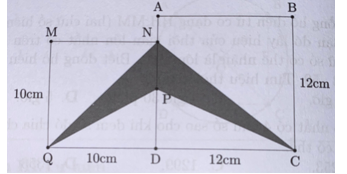
Cho hai hình vuông ABCD và MNDQ lần lượt có cạnh là 12 cm và 10 cm. Nói Q và B, gọi P là giao điểm của QB và AD. Tính diện tích hình tô đậm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Nối N với B và nối P với B.
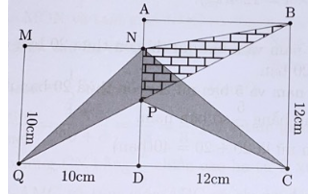
Ta có: SNPB = SNPC (hai tam giác chung đáy NP, chiều cao kẻ từ đỉnh B bằng chiều cao kẻ từ đỉnh C xuống đáy NP).
Vậy phần diện tích tô đậm SNCPQ = SNPQ + SNPB
Ta có: AN = 12 – 10 = 2 (cm); QC = 10 +12 = 22 (cm)
Diện tích hình vuông ABCD là
SABCD = 12 × 12 = 144 (cm2)
Diện tích hình vuông MNDQ là SMNDQ = 10 × 10 = 100 (cm2)
Diện tích tam giác MNQ là SMNQ = 10 × 10 : 2 = 50 (cm2)
Diện tích tam giác ABN là SABN = 12 × 2 : 2 = 12 (cm2)
Diện tích tam giác BQC là SBQC = 22 × 12 : 2 = 132 (cm2)
Vậy phần diện tích tô đậm là
SABCD + SMNDQ – SMNQ – SABN – SQBC = 144 + 100 – 50 –12 – 132 = 50 (cm2)Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
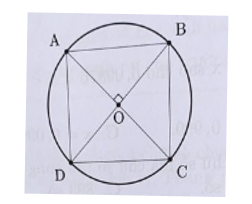
Gọi bán kính của hình tròn tâm O là r.
Ta có: r = OA = OB
Ta có r × r × 3,14 = 50,24
r × r = 50,24: 3,14
r × r = 16
Diện tích tam giác OAB là
SOAB = × OA × OB = × r × r = × 16 = 8 cm2
Vì SABCD = 4 × SOAB nên diện tích hình vuông ABCD là 8 × 4 = 32 cm2.Lời giải
Thể tích bể nước là 3 × 1,2 × 1,5 = 5,4 (m3)
Đổi: 5,4m3 = 5400 dm3 = 5400 (l)
Lượng nước trong bể hiện có là 5400 × 40 : 100 = 2160 (l)
Lượng nước trong bể sau khi đổ thêm là 5400 × 90 : 100 = 4860 (l)
Lượng nước cần phải đổ thêm là 4860 – 2160 = 2700 (l).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập