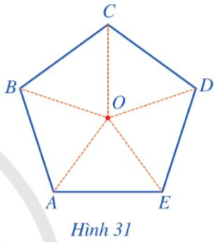
Cho hình ngũ giác đều ABCDE có tâm O (Hình 31).
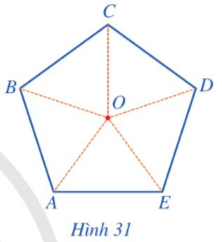
Phép quay ngược chiều tâm O biến điểm A thành điểm E thì các điểm B, C, D, E tương ứng biến thành các điểm nào?
Cho hình ngũ giác đều ABCDE có tâm O (Hình 31).

Câu hỏi trong đề: Giải SGK Toán 9 CD Bài 2. Phép quay có đáp án !!
Quảng cáo
Trả lời:
Vì ngũ giác đều ABCDE có tâm O nên OA = OB = OC = OD = OE.
Vì ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC.
Do đó ∆OAB = ∆OBC (c.c.c).
Chứng minh tương tự ta có
∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOA.
Suy ra ![]()
Mà ![]()
Do đó ![]()
Suy ra 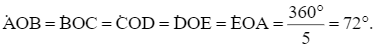
Như vậy, phép quay ngược chiều 72° tâm O giữ nguyên điểm O, biến điểm A thành điểm E thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OE, điểm A tạo nên cung AE có số đo 72°.
Khi đó, phép quay ngược chiều 72° tâm O biến các điểm B, C, D, E tương ứng thành các điểm A, B, C, D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
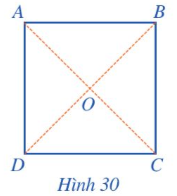
Vì ABCD là hình vuông nên AC = BD, AC ⊥ BD tại O và O là trung điểm của AC, BD.
Do đó OA = OB = OC = OD và ![]()
Ta có góc được tạo bởi khi quay tia OA đến tia OD thuận chiều quay của kim đồng hồ là: ![]()
Như vậy, phép quay thuận chiều 270° tâm O biến điểm A thành điểm D, biến các điểm B, C, D tương ứng thành các điểm A, B, C.
Lời giải
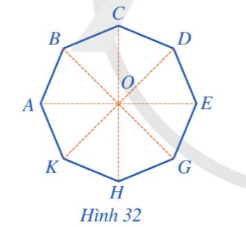
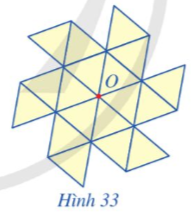
Hình đa giác đều ABCDEGHK có 8 cạnh nên ta có các phép quay thuận chiều α° tâm O và các phép quay ngược chiều α° tâm O, với α° lần lượt nhận các giá trị sau đây thì giữ nguyên đa giác đều đó:
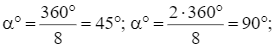
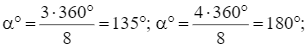
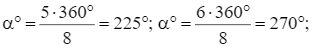
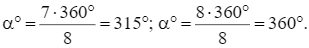
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.