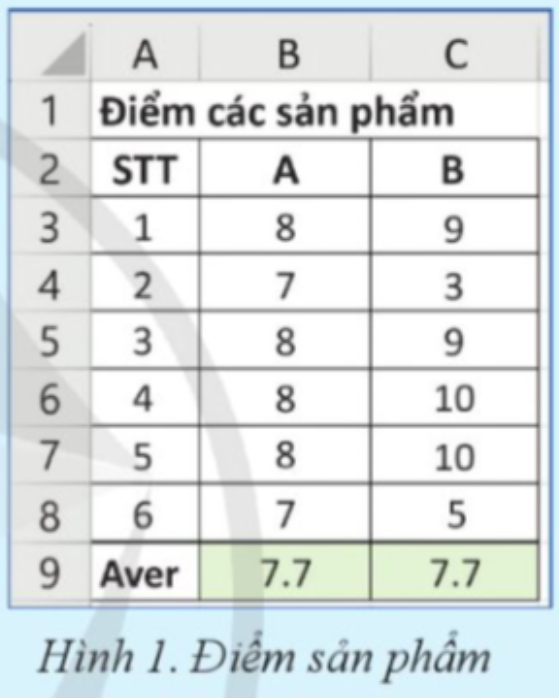
Coi dãy điểm của nhóm A và nhóm B trong bảng tính ở Hình 1 là các tập giá trị quan sát được của hai mẫu số liệu A và B. Hãy tính các số đặc trưng đo độ phân tán của các mẫu số liệu này trong Excel.

Xem lời giải

Câu hỏi trong đề: Giải chuyên đề Tin 12 Cánh diều Bài 6. Mô tả đặc trưng độ phân tán dữ liệu có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Coi dãy điểm của nhóm A và nhóm B trong bảng tính ở Hình 1 là các tập giá trị quan sát được của hai mẫu số liệu A và B. Để tính các số đặc trưng đo độ phân tán của các mẫu số liệu trong Excel và so sánh mức độ đại diện của điểm trung bình cho hai nhóm thì thực hiện các bước sau:

Tính các số đặc trưng đo độ phân tán cho mỗi nhóm như sau:

1. Độ lệch chuẩn (Standard Deviation): Nhóm A: =STDEV.P()

2. Phương sai (Variance): Nhóm A: =VAR.P()

3. Khoảng giá trị (Range): =MAX() - MIN()

4. Hệ số biến thiên (Coefficient of Variation): =(STDEV.P() / AVERAGE()) * 100

5. So sánh các giá trị: Nhóm nào có các giá trị đo độ phân tán (độ lệch chuẩn, phương sai, khoảng giá trị, hệ số biến thiên) nhỏ hơn thì điểm trung bình của nhóm đó đại diện tốt hơn cho các điểm số trong nhóm.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Trong các câu sau, những câu nào đúng về các hàm tính độ phân tán dữ liệu trong Excel?

a) Excel cung cấp các hàm trực tiếp tính khoảng biến thiên và hệ số biến thiên.

b) Sử dụng các hàm VAR.S, STDEV.S để tính phương sai và độ lệch chuẩn của một mẫu số liệu.

c) Sử dụng phương sai tốt hơn sử dụng độ lệch chuẩn khi giải thích sự sai khác giữa các giá trị trong mẫu với giá trị trung bình của mẫu.

d) Dãy số liệu nào có các số đặc trưng do độ phân tán càng lớn thì giá trị trung bình của dãy càng không đại diện tốt cho dãy đó.

Xem đáp án

Lời giải

a) Sai. Vì Excel không cung cấp các hàm trực tiếp tính khoảng biến thiên và hệ số biến thiên. Khoảng biến thiên (range) có thể tính bằng cách lấy giá trị lớn nhất trừ đi giá trị nhỏ nhất trong dãy số liệu (=MAX(range) - MIN(range)), và hệ số biến thiên (coefficient of variation) cần tính toán bằng cách chia độ lệch chuẩn cho trung bình và nhân với 100 để ra phần trăm (=(STDEV.S(range) / AVERAGE(range)) * 100).

b) Đúng. Vì trong Excel, VAR.S được sử dụng để tính phương sai của một mẫu và STDEV.S được sử dụng để tính độ lệch chuẩn của một mẫu.

c) Sai. Vì độ lệch chuẩn thường được sử dụng phổ biến hơn phương sai khi giải thích sự sai khác giữa các giá trị trong mẫu với giá trị trung bình của mẫu vì độ lệch chuẩn có cùng đơn vị đo với dữ liệu gốc, trong khi phương sai có đơn vị đo là bình phương của đơn vị gốc.

d) Đúng. Vì nếu một dãy số liệu có độ phân tán lớn (độ lệch chuẩn, phương sai lớn), thì giá trị trung bình của dãy không đại diện tốt cho các giá trị trong dãy vì các giá trị cá biệt có xu hướng cách xa trung bình nhiều hơn.

Câu 2

Bảng tính ở Hình 1 ghi lại điểm đánh giá các sản phẩm số của hai nhóm học sinh A và B trong một quá trình học tập. Ta thấy điểm trung bình (ở dòng cuối bảng) của hai nhóm đều bằng nhau (bằng 7.7). Theo em, cần tính những hàm nào trong Excel để từ đó kết luận được điểm trung bình của nhóm nào đại diện tốt hơn cho dãy điểm của nhóm?

Xem đáp án

Lời giải

Bảng tính ở Hình 1 ghi lại điểm đánh giá các sản phẩm số của hai nhóm học sinh A và B trong một quá trình học tập. Ta thấy điểm trung bình (ở dòng cuối bảng) của hai nhóm đều bằng nhau (bằng 7.7). Để xác định điểm trung bình của nhóm nào đại diện tốt hơn cho dãy điểm của nhóm đó, ta cần tính toán thêm một số hàm thống kê trong Excel để đánh giá sự phân bố và sự biến thiên của các điểm số. Một số hàm cụ thể như sau:

1. Hàm khoảng giá trị (Range):

Công thức: =Max(giá trị:giá trị) - Min(giá trị:giá trị)

Khoảng biến thiên của một mẫu số liệu là chênh lệch giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu. Khoảng biến thiên dùng để Sử dụng hàm MAX, MIN để tính khoảng biến thiên.

2. Hàm độ lệch chuẩn (Standard Deviation):

Công thức trong Excel: =STDEV.P(giá trị) hoặc =STDEV.S(giá trị)

Độ lệch chuẩn của một mẫu số liệu là căn bậc 2 của phương sai của mẫu đó. Độ lệch chuẩn phản ánh độ phân tán của một giá trị quan sát xung quanh giá trị trung bình.

3. Hàm tính hệ số biến thiên (Coefficcient of variation)

Công thức trong Excel: = STDEV.S(giá trị)/ ARAVERA(giá trị)

Hệ số biến thiên của một mẫu số liệu là tỉ lệ giữa độ lệch chuẩn và giá trị trung bình của mẫu.

Câu 3