Câu hỏi:
12/07/2024 1,082
Khi mua vé tham gia một trò chơi, người chơi được chọn một trong hai phương án sau:
- Phương án 1: Người chơi gieo một xúc xắc cân đối, đồng chất một cách độc lập liên tiếp 12 lần. Người chơi thắng nếu có ít nhất hai lần xúc xắc xuất hiện mặt 6 chấm.
- Phương án 2: Người chơi gieo một con xúc xắc cân đối, đồng chất một cách độc lập liên tiếp 6 lần. Người chơi thắng nếu có ít nhất một lần xúc xắc xuất hiện mặt 6 chấm.
Hỏi người chơi nên chọn phương án náo để xác suất thắng cao hơn?
Khi mua vé tham gia một trò chơi, người chơi được chọn một trong hai phương án sau:
- Phương án 1: Người chơi gieo một xúc xắc cân đối, đồng chất một cách độc lập liên tiếp 12 lần. Người chơi thắng nếu có ít nhất hai lần xúc xắc xuất hiện mặt 6 chấm.
- Phương án 2: Người chơi gieo một con xúc xắc cân đối, đồng chất một cách độc lập liên tiếp 6 lần. Người chơi thắng nếu có ít nhất một lần xúc xắc xuất hiện mặt 6 chấm.
Hỏi người chơi nên chọn phương án náo để xác suất thắng cao hơn?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Sau khi học xong bài này, ta giải quyết được bài toán này như sau:
Xác suất nếu người chơi chọn phương án 1:
Gọi T là phép thử: “Gieo một xúc xắc cân đối, đồng chất”;
E là biến cố: “Xúc xắc xuất hiện mặt 6 chấm”.
Xét phép thử lặp với n = 12 và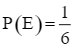 
.
Gọi B là biến cố: “Người chơi thắng”.
B cũng là biến cố: “Trong phép thử lặp T, với n = 12, biến cố E xuất hiện ít nhất hai lần”.
Xét biến cố đối 
: “Trong phép thử lặp T, biến cố E xuất hiện nhiều nhất một lần”.
Ta có 
. Theo quy tắc cộng xác suất và công thức bernoulli, ta có:
.
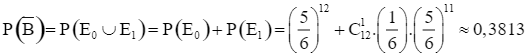Do đó P(B) = 1 – 0,3813 = 0,6187.
Xác suất nếu người chơi chọn phương án 2:
Gọi T là phép thử: “Gieo một xúc xắc cân đối, đồng chất”;
E là biến cố: “Xúc xắc xuất hiện mặt 6 chấm”.
Xét phép thử lặp với n = 6 và .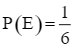
Gọi B là biến cố: “Người chơi thắng”.
B cũng là biến cố: “Trong phép thử lặp T, với n = 6, biến cố E xuất hiện ít nhất một lần”.
Xét biến cố đối : “Trong phép thử lặp T, biến cố E không xuất hiện”.
Khi đó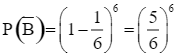 
.
Do đó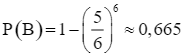 
.
Ta thấy người chơi nên chọn theo phương án 2 thì xác suất thắng cao hơn.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xác suất để An thắng trận đấu là xác suất để An thắng ít nhất hai ván đấu.
Gọi biến cố A: “An thắng trận đấu đó”.
Trường hợp 1: An thắng cả ba ván đấu
Khi đó ta có P1 = 0,43 = 0,064.
Trường hợp 2: An thắng 2 ván đấu.
Khi đó ta có: 
.
Vậy P(A) = P1 + P2 = 0,064 + 0,288 = 0,352.
Lời giải
X là số linh kiện không đạt tiêu chuẩn.
X là một biến ngẫu nhiên có phân bố nhị thức với tham số n = 10; p = 0,01.
Hộp được xếp loại I nếu hộp đó có nhiều nhất một linh kiện không đạt tiêu chuẩn tức là X ≤ 1.
Theo chú ý về phân bố nhị thức ta có:
.
Vậy tỉ lệ những hộp linh kiện điện tử loại I là 99,6%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận