Một công ty cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 10 chiếc và loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi xe loại A có thể chở tối đa 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn hàng. Phải thuê bao nhiêu xe loại A và bao nhiêu xe loại B để chi phí bỏ ra là ít nhất mà vẫn chở được hết hàng và người?
Một công ty cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 10 chiếc và loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu đồng. Biết rằng mỗi xe loại A có thể chở tối đa 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn hàng. Phải thuê bao nhiêu xe loại A và bao nhiêu xe loại B để chi phí bỏ ra là ít nhất mà vẫn chở được hết hàng và người?
Quảng cáo
Trả lời:
Gọi x và y lần lượt là số xe loại A và loại B cần thuê.
Chi phí thuê xe là: F(x; y) = 4x + 3y (triệu đồng).
Hệ bất phương trình ràng buộc x và y là:
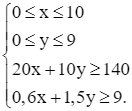
Miền nghiệm của hệ bất phương trình trên là miền tứ giác ABCD trong hình vẽ dưới đây:
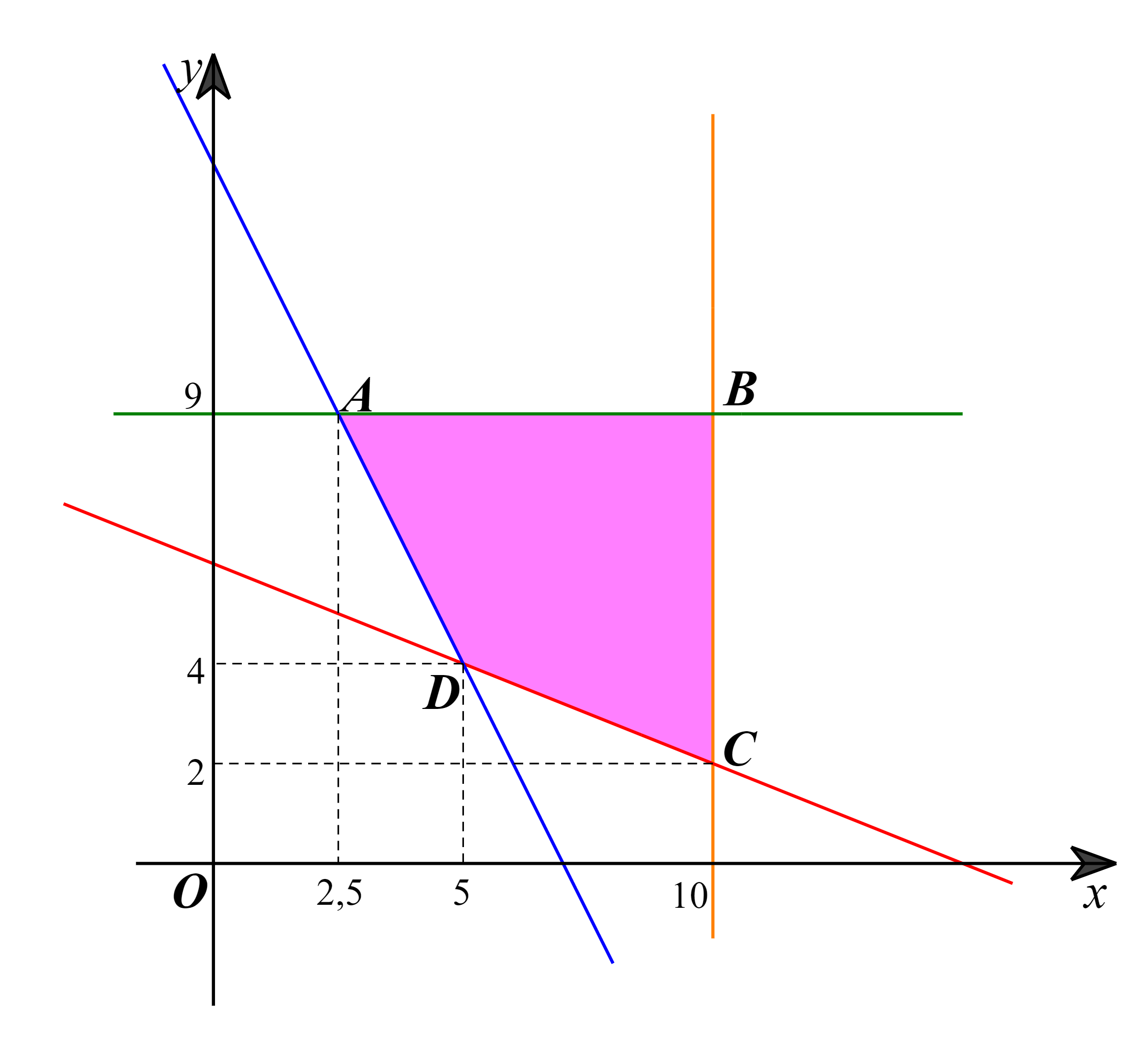
Các điểm cực biên là: A(2,5; 9), B(10; 9), C(10; 2), D(5; 4).
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền tứ giác ABCD. Ta biết rằng F(x; y) đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác. Tính giá trị củ F(x; y) tại các đỉnh của tứ giác ta được:
F(2,5; 9) = 4.2,5 + 3.9 = 37;
F(10; 9) = 4.10 + 3.9 = 67;
F(10; 2) = 4.10 + 3.2 = 46;
F(5; 4) = 4.5 + 3.4 = 32.
Giá trị nhỏ nhất của F(x; y) bằng 32 tại D(5; 4). Phương án tối ưu là (5; 4).
Vậy phải thuê 5 xe loại A và 4 xe loại B để chi phí bỏ ra là ít nhất (32 triệu đồng) mà vẫn chở được hết hàng và người.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x và y lần lượt là số bàn hình chữ nhật và số bàn tròn cần thuê.
Chi phí thuê bàn là: 200x + 300y (nghìn đồng).
Hệ bất phương trình ràng buộc x và y là
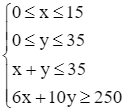 hay
hay 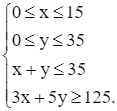
Miền nghiệm của hệ bất phương trình này là miền tứ giác ABCD được tô màu như hình vẽ dưới đây:
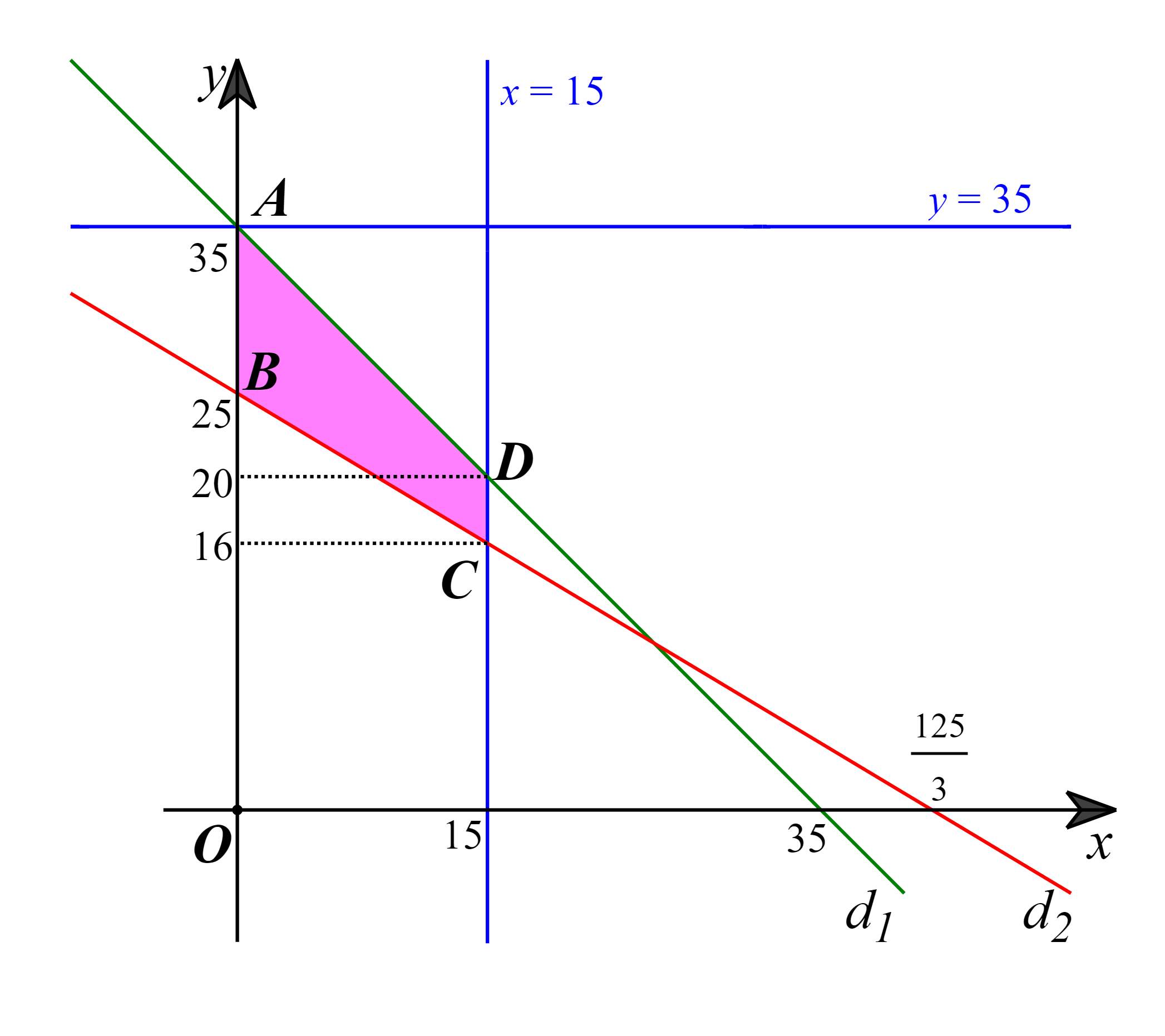
Ở đây, d1: x + y = 35 và d2: 3x + 5y = 125.
Các điểm cực biên là: A(0; 35), B(0; 25), C(15; 16), D(15; 20).
Bài toán yêu cầu tìm giá trị nhỏ nhất của F(x; y) trên miền nghiệm của hệ bất phương trình trên. Ta biết rằng, F(x; y) đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác. Tính giá trị của F(x; y) tại các điểm cực biên ta được:
F(0; 35) = 200.0 + 300.35 = 10 500;
F(0; 25) = 200.0 + 300.25 = 7 500;
F(15; 16) = 200.15 + 300.16 = 7 800;
F(15; 20) = 200.15 + 300.20 = 9 000.
Giá trị nhỏ nhất của F(x; y) bằng 7 500 tại điểm cực biên B(0; 25). Phương án tối ưu là (0; 25).
Vậy anh Nam chỉ cần thuê 25 bàn tròn để giảm thiểu tối đa chi phí mà vẫn đáp ứng được các yêu cầu trên.
Lời giải
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Gọi x và y lần lượt là số kilôgam sản phẩm loại I và loại II cần sản xuất.
Lợi nhuận của xí nghiệp khi sản xuất x kg sản phẩm loại I và y kg sản phẩm loại II là: F(x; y) = 40x + 30y (nghìn đồng).
Số kg nguyên liệu để sản xuất x kg sản phẩm loại I và y kg loại II là: 2x + 4y (kg).
Số giờ làm để sản xuất x kg sản phẩm loại I và y kg loại II là: 30x + 15y (giờ).
Vì xí nghiệp có 200 kg nguyên liệu (lượng nguyên liệu sử dụng không vượt quá lượng có sẵn) và tối đa 1 200 giờ làm việc nên ta có hệ:
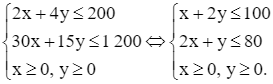
Miền nghiệm của hệ bất phương trình trên là miền tứ giác OABC được tô màu trong hình vẽ dưới đây, trong đó đường thẳng d1: x + 2y = 100 và đường thẳng d2: 2x + y = 80.
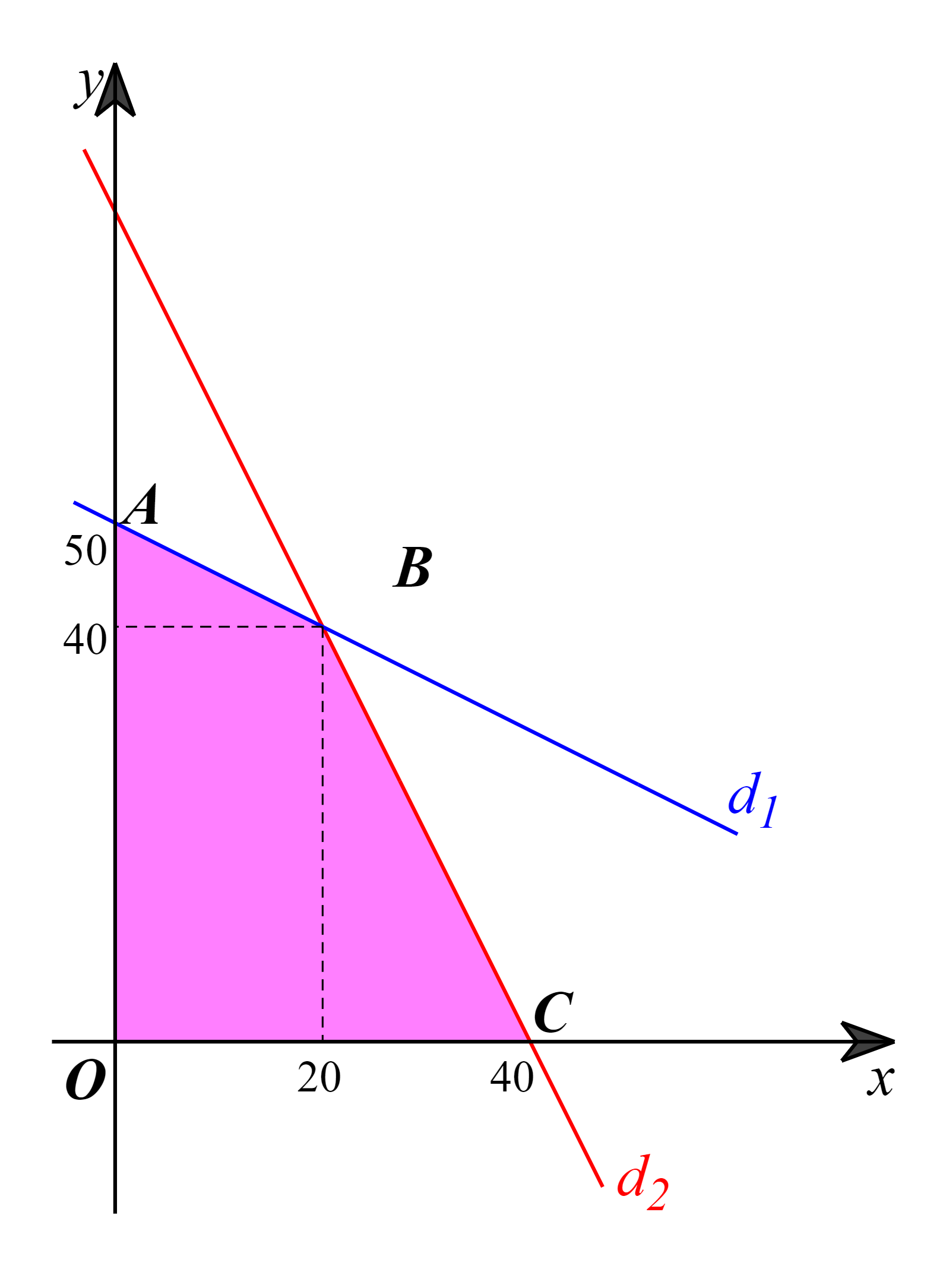
Các điểm cực biên là: O(0; 0), A(0; 50), B(20; 40), C(40; 0).
Bài toán yêu cầu tìm giá trị lớn nhất của F(x; y) trên miền tứ giác OABC. Tính giá trị của F(x; y) tại các đỉnh của tứ giác, ta được:
F(0; 0) = 40.0 + 30.0 = 0;
F(0; 50) = 40.0 + 30.50 = 1 500;
F(20; 40) = 40.20 + 30.40 = 2 000;
F(40; 0) = 40.40 + 30.0 = 1 600.
Giá trị lớn nhất của F(x; y) bằng 2 000 tại (20; 40). Phương án tối ưu là (20; 40).
Vậy lợi nhuận cao nhất mà xí nghiệp đạt được là 2 000 nghìn đồng, tức 2 triệu đồng khi sản xuất 20 kg sản phẩm loại I và 40 kg sản phẩm loại II.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.