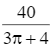Câu hỏi:
12/07/2024 18,528
Một xe khách tuyến có sức chứa tối đa là 60 hành khách. Nếu chuyến xe chở x hành khách thì giá cho mỗi hành khách là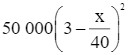 
(đồng). Xe có doanh thu cao nhất khi chở bao nhiêu hành khách, và doanh thu đó bằng bao nhiêu?
Một xe khách tuyến có sức chứa tối đa là 60 hành khách. Nếu chuyến xe chở x hành khách thì giá cho mỗi hành khách là 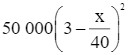(đồng). Xe có doanh thu cao nhất khi chở bao nhiêu hành khách, và doanh thu đó bằng bao nhiêu?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hàm doanh thu khi chở x khách hàng là:
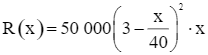
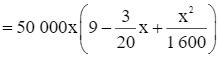
= 450 000x – 7 500x2 + 31,25x3 (đồng) với 0 ≤ x ≤ 60.
Đạo hàm của hàm R(x) là: R’(x) = 450 000 – 15 000x + 93,75x2.
R’(x) = 0 ⇔ 450 000 – 15 000x + 93,75x2 = 0
⇔ x = 120 (không thuộc [0; 60]) hoặc x = 40 (thỏa mãn).
Vận dụng phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một đoạn, ta có:
R(0) = 0; R(40) = 8 000 000; R(60) = 6 750 000.
Vì giá trị R(40) là giá trị lớn nhất trong ba giá trị trên, nên giá trị lớn nhất của R(x) đạt được khi x = 40.
Vậy xe có doanh thu cao nhất khi chở 40 hành khách và doanh thu đó bằng 8 000 000 đồng.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hàm doanh thu là: R(x) = x.p(x) = x.(1 500 – 3x) = 1 500x – 3x2 (nghìn đồng).
Hàm lợi nhuận là:
P(x) = R(x) – C(x) = 1 500x – 3x2 – (18 000 + 500x – 1,6x2 + 0,004x3)
= 1 500x – 3x2 – 18 000 – 500x + 1,6x2 – 0,004x3
= – 0,004x3 – 1,4x2 + 1 000x – 18 000.
Vậy công thức của hàm lợi nhuận là P(x) = – 0,004x3 – 1,4x2 + 1 000x – 18 000 (nghìn đồng).
Lời giải
Gọi x (m) là chiều rộng của hình chữ nhật, 0 < x < 10.
Khi đó, bán kính của phần cửa sổ nửa hình tròn là 
(m).
Diện tích của phần cửa sổ nửa hình tròn là: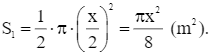 
Độ dài mép ngoài của phần cửa nửa đường tròn chính là nửa chu vi đường tròn và bằng: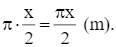 
Độ dài mép ngoài của phần cửa hình chữ nhật và cũng là chu vi hình chữ nhật, bằng:
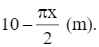
Chiều dài của phần cửa sổ hình chữ nhật là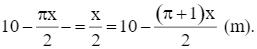 
Diện tích của phần cửa sổ hình chữ nhật là:
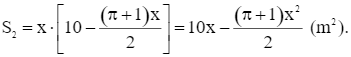
Diện tích của cửa sổ là:
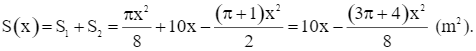
Xét hàm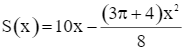 
trên khoảng (0; 10).
Ta có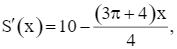 
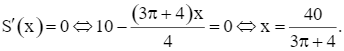
Lập bảng biến thiên của hàm số trên khoảng (0; 10):
|
0 |
|
|
|
10 |
|
|
|
|
+ |
0 |
– |
|
|
|
0 |
|
14,90
|
|
–67,81 |
Từ bảng biến thiên, ta có 
khi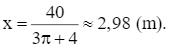 
Vậy các kích thước của hình chữ nhật lần lượt là khoảng 2,98 m và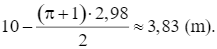 
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)