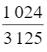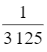Cho biến ngẫu nhiên rời rạc X có phân bố nhị thức B(5; 0,2).
Tính kì vọng và độ lệch chuẩn của X.
Cho biến ngẫu nhiên rời rạc X có phân bố nhị thức B(5; 0,2).
Quảng cáo
Trả lời:
Ta có ![]() với k = 0, 1, 2, 3, 4, 5.
với k = 0, 1, 2, 3, 4, 5.
Lần lượt tính P(X = k) với k = 0, 1, 2, 3, 4, 5 từ công thức trên, ta thu được bảng phân bố xác suất của X như sau:
|
X |
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
|
|
|
|
|
|
Kì vọng của X là:
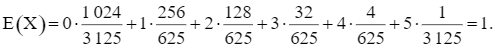
Phương sai của X là:
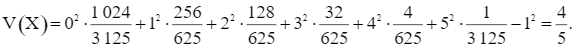
Độ lệch chuẩn của X là:
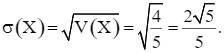
Chú ý: Ta cũng có thể tính kì vọng và phương sai của X như sau:
E(X) = np = 5 . 0,2 = 1 và V(X) = np(1 – p) = 5 . 0,2 . (1 – 0,2) = 0,8.
Do đó độ lệch chuẩn của X là: 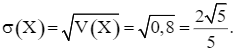
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi T là phép thử “Phỏng vấn ngẫu nhiên một người lao động từ khi công nghiệp”. Theo đề bài, phép thử T được lặp lại 10 lần một cách độc lập. Gọi X là biến cố “Người lao động có bằng đại học”. Ta có P(X) = 30% = 0,3.
Gọi Xk là biến cố “Có k người có bằng đại học trong 10 người lao động được phỏng vấn”, với k = 0, 1, …, 10. Áp dụng công thức Bernoulli, ta có:
![]() với k = 0, 1, …, 10.
với k = 0, 1, …, 10.
Do đó, ![]()
Ta có ![]()
Lời giải
Gọi T là phép thử “Chọn ngẫu nhiên một người”. Theo đề bài, phép thử T được lặp lại 8 lần một cách độc lập. Gọi A là biến cố “Người đó có nhóm máu O”. Ta có P(A) = 40% = 0,4.
Gọi X là số người có nhóm máu O trong 8 người được chọn.
Do phép thử T được thực hiện 8 lần một cách độc lập với nhau và xác suất xảy ra biến cố A trong mỗi lần thử đều bằng 0,4 nên X là biến cố ngẫu nhiên rời rạc có phân bố nhị thức B(8; 0,4). Do đó:
![]() với k = 0, 1, …, 8.
với k = 0, 1, …, 8.
Xác suất để có đúng 3 người được chọn có nhóm máu O là:
![]()
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.