Một cửa hàng kinh doanh tổ chức rút thăm trúng thưởng cho hai loại sản phẩm. Tỉ lệ trúng thưởng của các loại sản phẩm I, II lần lượt là: 6%; 4%. Trong một hộp kín gồm các thăm cùng loại, người ta để lẫn lộn 200 chiếc thăm cho sản phẩm loại I và 300 chiếc thăm cho sản phẩm loại II. Một khách hàng lấy ngẫu nhiên 1 chiếc thăm từ chiếc hộp đó.
Tính xác suất để chiếc thăm được lấy ra là trúng thưởng.
Câu hỏi trong đề: Giải SGK Toán 12 CD Bài tập cuối chương 6 có đáp án !!
Quảng cáo
Trả lời:
Xét hai biến cố:
A: “Chiếc thăm được lấy ra là trúng thưởng”;
B: “Chiếc thăm được lấy ra là chiếc thăm cho sản phẩm loại I”.
Vì người ta để lẫn lộn 200 chiếc thăm cho sản phẩm loại I và 300 chiếc thăm cho sản phẩm loại II nên P(B) = 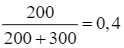 và P(
và P(![]() ) = 1 – 0,4 = 0,6.
) = 1 – 0,4 = 0,6.
Do tỉ lệ trúng thưởng của các loại sản phẩm I, II lần lượt là: 6%; 4% nên
P(A | B) = 0,06 và P(A | ![]() ) = 0,04.
) = 0,04.
Xác suất để chiếc thăm được lấy ra là trúng thưởng là:
P(A) = P(B) ∙ P(A | B) + P(![]() ) ∙ P(A |
) ∙ P(A | ![]() ) = 0,4 ∙ 0,06 + 0,6 ∙ 0,04 = 0,048.
) = 0,4 ∙ 0,06 + 0,6 ∙ 0,04 = 0,048.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Xét hai biến cố:
A: “Bạn Ngân lấy được viên bi màu vàng ở lần lấy thứ nhất”;
B: “Bạn Ngân lấy được viên bi màu vàng ở lần lấy thứ hai”.
Khi đó, xác suất để cả hai lần bạn Ngân đều lấy ra được viên bi màu vàng chính là xác suất có điều kiện P(B | A).
Lấy một viên bi lần thứ nhất có 40 cách chọn, viên bi được lấy ra không bỏ lại hộp nên lấy một viên bi lần thứ hai có 39 cách chọn. Do đó n(Ω) = 40 ∙ 39.
Bạn Ngân lấy được viên bi màu vàng ở lần lấy thứ nhất thì có 28 cách chọn, ở lần lấy thứ hai có 39 cách chọn. Do đó, n(A) = 28 ∙ 39.
Bạn Ngân lấy được viên bi màu vàng ở lần lấy thứ nhất thì có 28 cách chọn, lấy ra viên bi màu vàng ở lần lấy thứ hai có 27 cách chọn. Do đó, n(A ∩ B) = 28 ∙ 27.
Khi đó, P(B | A) = 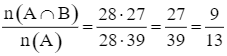 .
.
Vậy xác suất để cả hai lần bạn Ngân đều lấy ra được viên bi màu vàng là ![]() .
.
Lời giải
Đáp án đúng là: D
Vì A và B là hai biến cố xung khắc nên A ∩ B = ∅, do đó P(A ∩ B) = 0.
Khi đó, P(A | B) = 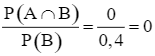 .
.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.