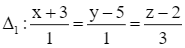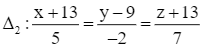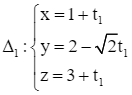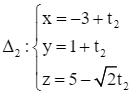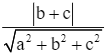Câu hỏi trong đề: Giải SGK Toán 12 CD Bài tập cuối chương 5 có đáp án !!
Quảng cáo
Trả lời:
Đường thẳng ∆1 đi qua điểm M1(– 3; 5; 2) và có ![]() là vectơ chỉ phương.
là vectơ chỉ phương.
Đường thẳng ∆2 đi qua điểm M2(– 13; 9; – 13) và có ![]() là vectơ chỉ phương.
là vectơ chỉ phương.
Ta có 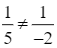 , suy ra hai vectơ
, suy ra hai vectơ ![]() không cùng phương.
không cùng phương.
![]() ,
, 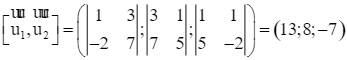 .
.
Do ![]() 13 ∙ (– 10) + 8 ∙ 4 + (– 7) ∙ (– 15) = 7 ≠ 0 nên
13 ∙ (– 10) + 8 ∙ 4 + (– 7) ∙ (– 15) = 7 ≠ 0 nên ![]() không đồng phẳng.
không đồng phẳng.
Vậy ∆1 và ∆2 chéo nhau.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương trình tham số của đường thẳng d đi qua điểm A(– 688; – 185; 8) và có vectơ chỉ phương ![]() là:
là: 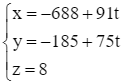 (t là tham số).
(t là tham số).
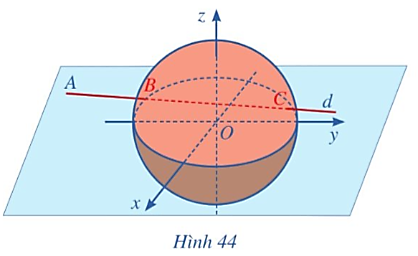
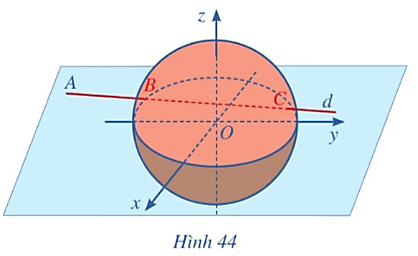
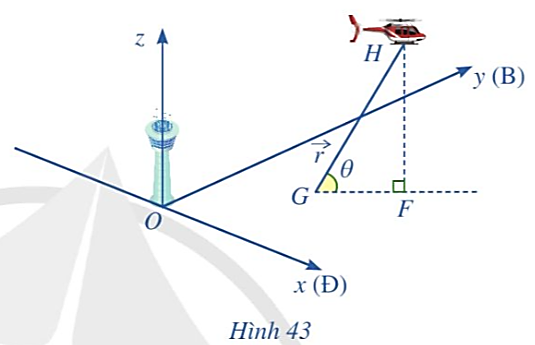
Gọi B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa.
Vì B ∈ d nên B(– 688 + 91t; – 185 + 75t; 8).
B là vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa khi OB = 417, tức là
![]()
⇔ 13 906t2 – 152 966t + 333 744 = 0
⇔ t = 3 hoặc t = 8.
+ Với t = 3, ta có B(– 415; 40; 8).
Khi đó AB = ![]() .
.
+ Với t = 8, ta có B(– 88; 415; 8).
Khi đó AB = ![]() .
.
Vì 353,77 < 848,53 nên tọa độ vị trí sớm nhất mà máy bay xuất hiện trên màn hình ra đa là (– 415; 40; 8).
Lời giải
Gọi H là vị trí mà máy bay bay gần đài kiểm soát không lưu nhất. Khi đó, khoảng OH phải ngắn nhất, điều này xảy ra khi và chỉ khi OH ⊥ d.
Vì H ∈ d nên H(– 688 + 91t'; – 185 + 75t'; 8).
Ta có ![]() (– 688 + 91t'; – 185 + 75t'; 8).
(– 688 + 91t'; – 185 + 75t'; 8).
OH ⊥ d ![]()
⇔ (– 688 + 91t') ∙ 91 + (– 185 + 75t') ∙ 75 + 8 ∙ 0 = 0
⇔ 13 906t' – 76 483 = 0 ⇔ t' = ![]() .
.
Suy ra H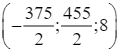 .
.
Khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó là:
OH = 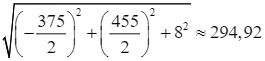 (km).
(km).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.