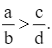Câu hỏi trong đề: Giải SBT Toán 9 CD Bài tập cuối chương 2 có đáp án !!
Quảng cáo
Trả lời:
Xét hiệu:
(a2 + 1)(b2 + 1) ‒ 4ab
= a2b2 + a2 + b2 + 1 ‒ 4ab
= (a2b2 ‒ 2ab + 1) + (a2 ‒2ab + b2)
= (ab ‒ 1)2 + (a ‒ b)2.
Với hai số thực a, b tùy ý, ta có: (ab ‒ 1)2 ≥ 0 và (a ‒ b)2 ≥ 0.
Suy ra: (ab ‒ 1)2 + (a ‒ b)2 ≥ 0 hay (a2 + 1)(b2 + 1) ‒ 4ab ≥ 0.
Vậy (a2 + 1)(b2 + 1) ≥ 4ab.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số tiền nhóm khách A phải trả là:
11 000 + 14 500.29 + 11 600.(45 ‒ 30) = 605 500 (đồng).
Số tiền nhóm khách ![]() phải trả là:
phải trả là:
11 000 + 15 500.29 + 13 600.(40 ‒ 30) = 596 500 (đồng).
Số tiền nhóm khách A phải trả nhiều hơn số tiền nhóm khách B phải trả là:
605 500 ‒ 596 500 = 9 000 (đồng).
Do 9 000 < 10 000 nên nhận định đã cho là sai.
Lời giải
Gọi x là số phút gọi ngoại mạng của bác Lan trong tháng 10 (x > 0).
Số tiền bác Lan sử dụng để gọi ngoại mạng là: 2 000x (đồng).
Số tiền bác Lan sử dụng 90 phút gọi nội mạng là: 1 200.90 = 108 000 (đồng).
Tổng tiền cước bác Lan phải trả trong tháng 10 là:
108 000 + 2 000x (đồng).
Do tiền cước bác Lan phải trả trong tháng 10 không vượt quá 200 000 đồng nên ta có bất phương trình:
108 000 + 2000x ≤ 200 000.
Giải bất phương trình:
108 000 + 2 000x ≤ 200 000
2 000x ≤ 200 000 ‒ 108 000
2 000x ≤ 9 200
x ≤ 46.
Vậy bác Lan có thể sử dụng nhiều nhất 46 phút gọi ngoại mạng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.