Cho đa giác đều 20 đỉnh. Lấy ngẫu nhiên 3 đỉnh từ 20 đỉnh trên. Tính xác suất để 3 đỉnh đó là 3 đỉnh của 1 tam giác không vuông cân.
A. 
.
. B. 
.
.C. 
.
.D. 
.
.Quảng cáo
Trả lời:
Giải bởi Vietjack
Số tam giác được tạo thành từ 20 đỉnh là 
tam giác. Đa giác đều 20 đỉnh có 10 đường chéo đi qua tâm đa giác. Cứ đường đường chéo tạo thành 1 hình chữ nhật, và 1 hình chữ nhật tạo thành 4 tam giác vuông nên có 
tam giác vuông.
Lại có, mỗi đỉnh trong 20 đỉnh sẽ là đỉnh của 1 tam giác vuông cân, nên số tam giác vuông cân được tạo thành từ 20 đỉnh là 20. Vậy số tam giác không vuông cân là 180 – 20 = 160.
Vậy xác suất để chọn được 1 tam giác không vuông cân là: 
. Chọn C.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 15 đề thi Đánh giá tư duy Đại học Bách Khoa Hà Nội 2025 (Tập 1) ( 39.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia TP Hồ Chí Minh (2 cuốn) ( 140.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. 
B. 
C. 
D. Không thể xác định.
Lời giải
Do đun nóng nước lọc lại thu được thêm kết tủa nên nước lọc có chứa 
Các phản ứng xảy ra khi cho sản phẩm cháy vào bình đựng dung dịch 
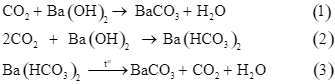
Ta có: 
; 
; 
Theo (2) và (3) ⟹ 
Theo (1) và (2) ⟹ 
Mặt khác, khối lượng dung dịch giảm 5,5 gam nên ta có:
Bảo toàn nguyên tố O ta có: 
Bảo toàn nguyên tố C, H ta có: 
Gọi CTPT của X là 
⟹ CTĐGN là 
CTPT của X có dạng 
Trong hợp chất hữu cơ chứa C, H, O ta luôn có:
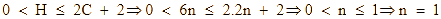
Vậy công thức phân tử của X là 
Chọn B.
Câu 2
A. Làm phức tạp các vấn đề xung đột.
B. Gia tăng nạn khủng bố trên thế giới.
C. Làm suy giảm chất lượng cuộc sống.
D. Đẩy nhanh tốc độ biến đối khí hậu.
Lời giải
Mất an ninh lương thực liên quan trực tiếp đến làm suy giảm chất lượng cuộc sống. Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Màu của tóc.
B. Người con gái.
C. Cái đẹp.
D. Tuổi trẻ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
.A. 0 < m < 2.
B. m > 0.
C. 0 < m < 4.
D. m < 9.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. 11,2%.
B. 12,2%.
C. 15,0%.
D. 29,4%.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo