Câu hỏi:

22/07/2024 1,265

* Mục đích:

Đo được tần số và điện áp xoay chiều bằng dụng cụ thực hành.

* Dụng cụ:

- Biến áp nguồn có điện áp đầu ra xoay chiều và có thể thay đổi được (1).

- Đồng hồ đo điện đa năng hiện số có chức năng đo lần số (2).

- Que đo đồng hồ đa năng (3).

* Tiến hành thí nghiệm

Bước 1: Cắm biến áp nguồn vào ổ điện 220 V - 50 Hz. Bật công tắc cho biến áp hoạt động. Vặn núm xoay phía trước để điều chỉnh điện áp đầu ra xoay chiều.

Bước 2: Ấn nút ON/OFF để đồng hồ đo điện đa năng hoạt động, vặn núm xoay để điều chỉnh chế độ đo điện áp xoay chiều.

Bước 3: Cắm hai dây nối của que đo vào đồng hồ đo điện đa năng.

Bước 4: Cắm hai đầu kim nhọn của hai dây nối vào hai lỗ cắm đầu ra của biến áp nguồn. Quan sát số chỉ điện áp hiệu dụng và tần số trên mặt đồng hồ đo. Khi các số chỉ ổn định, ghi lại hai giá trị này vào vở theo mẫu Bảng 1.1. Rút hai đầu kim nhọn ra khỏi biến áp nguồn.

Bước 5: Lặp lại bước 4 hai lần.

Bước 6: Tắt biến áp nguồn và rút phích cắm khỏi ổ điện. Tắt đồng hồ đo.

- Xác định độ chia nhỏ nhất của phép đo tần số, điện áp trên đồng hồ.

- Tính giá trị trung bình, sai số và viết kết quả. Nhận xét giá trị tần số đo được với tần số đã biết của mạng lưới điện.

Xem lời giải

Câu hỏi trong đề: Chuyên đề Vật lí 12 CTST Bài 1. Các đặc trưng của chiều dòng điện xoay chiều có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lần đo	U(V)	f(Hz)
1	9,012	50,03
2	9,005	49,97
3	8,995	50,05
Giá trị trung bình	9,004	50,02

Giá trị trung bình của điện áp: \[\overline U = \frac{{9,012 + 9,005 + 8,995}}{3} = 9,004\,V\]

Sai số tuyệt đối ứng với các lần đo điện áp:

\[\Delta {U_1} = \left| {\overline U - {U_1}} \right| = 0,008\]

\[\Delta {U_2} = \left| {\overline U - {U_2}} \right| = 0,001\]

\[\Delta {U_3} = \left| {\overline U - {U_3}} \right| = 0,009\]

Sai số tuyệt đối trung bình của 3 lần đo: \[\overline {\Delta U} = \frac{{\Delta {U_1} + \Delta {U_2} + \Delta {U_3}}}{3} = 0,006\]

Sai số tuyệt đối của phép đo: \[\Delta U = \overline {\Delta U} + \Delta {U_{dc}} = 0,006\]

Kết quả phép đo: \[U = 9,004 \pm 0,006\,V\]

Giá trị trung bình của tần số: \[\overline f = \frac{{50,03 + 49,97 + 50,05}}{3} \approx 50,02\,Hz\]

Sai số tuyệt đối ứng với các lần đo tần số:

\[\Delta {f_1} = \left| {\overline f - {f_1}} \right| = 0,01\]

\[\Delta {f_2} = \left| {\overline f - {f_2}} \right| = 0,05\]

\[\Delta {f_3} = \left| {\overline f - {f_3}} \right| = 0,03\]

Sai số tuyệt đối trung bình của 3 lần đo: \[\overline {\Delta f} = \frac{{\Delta {f_1} + \Delta {f_2} + \Delta {f_3}}}{3} = 0,03\]

Sai số tuyệt đối của phép đo: \[\Delta f = \overline {\Delta f} + \Delta {f_{dc}} = 0,03\]

Kết quả phép đo: \[f = 50,02 \pm 0,03\,Hz\]

Giá trị tần số đo được với tần số đã biết của mạng lưới điện gần bằng nhau.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Từ đồ thị cường độ của dòng điện xoay chiều theo thời gian ở Hình 1.2, hãy xác định:

a) Biên độ, tần số, chu kì, tần số góc, pha ban đầu, cường độ dòng điện hiệu dụng.

b) Biểu thức cường độ dòng điện tức thời.

c) Khoảng thời gian cường độ dòng điện tăng trong chu kì đầu tiên.

Xem đáp án

Lời giải

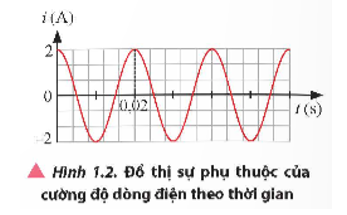
a) Biên độ I₀ = 2 A

Chu kì T = 0,02 s

Tần số \[f = \frac{1}{T} = 50\,Hz\]

Tần số góc \[\omega = 2\pi f = 100\pi \,(rad/s)\]

Pha ban đầu φ = 0 rad

Cường độ dòng điện hiệu dụng \[I = \frac{{{I_0}}}{{\sqrt 2 }} = \sqrt 2 A\]

b) Biểu thức cường độ dòng điện: \[i = 2\cos (100\pi t)A\]

c) Khoảng thời gian cường độ dòng điện tăng trong chu kì đầu tiên từ 0,01 s đến 0,02 s (ứng với nửa chu kì sau).

Câu 2

Hãy viết biểu thức cường độ dòng điện và điện áp xoay chiều. Giải thích các đại lượng. So sánh giá trị hiệu dụng và giá trị cực đại của cường độ dòng điện, điện áp.

Xem đáp án

Lời giải

Biểu thức cường độ dòng điện: \[i = {I_0}\cos (\omega t + {\varphi _i})\]

i: cường độ dòng điện tức thời, tức là cường độ dòng điện tại thời điểm t

I₀: cường độ dòng điện cực đại

ω: tần số góc

φ_i: pha ban đầu của cường độ dòng điện

Giá trị hiệu dụng \[I = \frac{{{I_0}}}{{\sqrt 2 }}\]

Biểu thức điện áp: \[u = {U_0}\cos (\omega t + {\varphi _u})\]

u: điện áp tức thời, tức là điện áp tại thời điểm t

U₀: điện áp cực đại

ω: tần số góc

φ_u: pha ban đầu của điện áp

Giá trị hiệu dụng \[U = \frac{{{U_0}}}{{\sqrt 2 }}\]

Câu 3