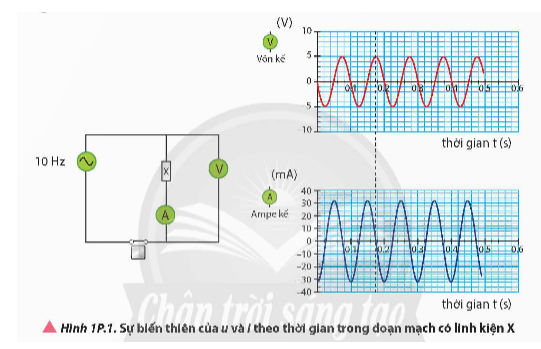
Dựa vào biểu thức cảm kháng ZL = ωL, tìm mối quan hệ giữa u và i khi đặt điện áp không đổi vào hai đầu cuộn cảm thuần.
Dựa vào biểu thức cảm kháng ZL = ωL, tìm mối quan hệ giữa u và i khi đặt điện áp không đổi vào hai đầu cuộn cảm thuần.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Điện áp đặt vào 2 đầu cuộn cảm thuần: \[u = {U_0}\cos \left( {\omega t + {\varphi _u}} \right)\]
Cường độ dòng điện: \[i = \frac{u}{{{Z_L}}} = \frac{{{U_0}}}{{{Z_L}}}\cos \left( {\omega t + {\varphi _u} - \frac{\pi }{2}} \right) = {I_0}\cos \left( {\omega t + {\varphi _i}} \right)\]
Pha ban đầu của cường độ dòng điện: \[{\varphi _i} = {\varphi _u} - \frac{\pi }{2}\]
Cường độ dòng điện cực đại: \[{I_0} = \frac{{{U_0}}}{{{Z_L}}} = \frac{{{U_0}}}{{\omega L}}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
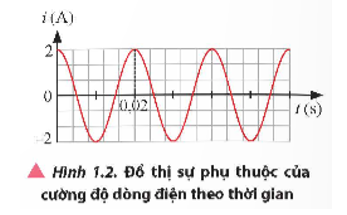
a) Biên độ I0 = 2 A
Chu kì T = 0,02 s
Tần số \[f = \frac{1}{T} = 50\,Hz\]
Tần số góc \[\omega = 2\pi f = 100\pi \,(rad/s)\]
Pha ban đầu φ = 0 rad
Cường độ dòng điện hiệu dụng \[I = \frac{{{I_0}}}{{\sqrt 2 }} = \sqrt 2 A\]
b) Biểu thức cường độ dòng điện: \[i = 2\cos (100\pi t)A\]
c) Khoảng thời gian cường độ dòng điện tăng trong chu kì đầu tiên từ 0,01 s đến 0,02 s (ứng với nửa chu kì sau).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Biểu thức cường độ dòng điện: \[i = {I_0}\cos (\omega t + {\varphi _i})\]
i: cường độ dòng điện tức thời, tức là cường độ dòng điện tại thời điểm t
I0: cường độ dòng điện cực đại
ω: tần số góc
φi: pha ban đầu của cường độ dòng điện
Giá trị hiệu dụng \[I = \frac{{{I_0}}}{{\sqrt 2 }}\]
Biểu thức điện áp: \[u = {U_0}\cos (\omega t + {\varphi _u})\]
u: điện áp tức thời, tức là điện áp tại thời điểm t
U0: điện áp cực đại
ω: tần số góc
φu: pha ban đầu của điện áp
Giá trị hiệu dụng \[U = \frac{{{U_0}}}{{\sqrt 2 }}\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập