Tứ giác ABCD có hai góc đối diện B và D vuông, hai góc kia không vuông.
a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Ta gọi đó là đường tròn (𝒞).
b) Gọi I và K lần lượt là trung điểm các đường chéo AC và BD của tứ giác. Chứng minh rằng IK ⊥ BD.
c) Kí hiệu các tiếp tuyến của đường tròn (𝒞) tại A, B và C lần lượt là a, b và c. Giả sử b cắt a và c theo thứ tự tại E và F. Chứng minh rằng tứ giác AEFC là một hình thang.
d) Chứng minh rằng EF = AE + CF.
Tứ giác ABCD có hai góc đối diện B và D vuông, hai góc kia không vuông.
a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Ta gọi đó là đường tròn (𝒞).
b) Gọi I và K lần lượt là trung điểm các đường chéo AC và BD của tứ giác. Chứng minh rằng IK ⊥ BD.
c) Kí hiệu các tiếp tuyến của đường tròn (𝒞) tại A, B và C lần lượt là a, b và c. Giả sử b cắt a và c theo thứ tự tại E và F. Chứng minh rằng tứ giác AEFC là một hình thang.
d) Chứng minh rằng EF = AE + CF.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Bài tập ôn tập cuối năm có đáp án !!
Quảng cáo
Trả lời:
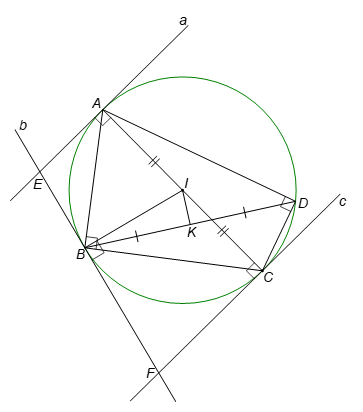
a) Xét ∆ABC vuông tại B nên đường tròn ngoại tiếp tam giác này có tâm là trung điểm của cạnh huyền AC. Do đó ba điểm A, B, C cùng nằm trên đường tròn đường kính AC.
Xét ∆ADC vuông tại D nên đường tròn ngoại tiếp tam giác này có tâm là trung điểm của cạnh huyền AC. Do đó ba điểm A, D, C cùng nằm trên đường tròn đường kính AC.
Vậy bốn điểm A, B, C và D cùng nằm trên đường tròn đường kính AC.
b) Do đường tròn (𝒞) đi qua bốn điểm A, B, C, D có đường kính là AC mà I là trung điểm của AC nên đường tròn (𝒞) có tâm là I, do đó IB = ID. Suy ra I nằm trên đường trung trực của BD.
Lại có K là trung điểm của BD nên K thuộc đường trung trực của BD.
Vì vậy, IK là đường trung trực của BD nên IK ⊥ BD.
c) Vì đường thẳng a là tiếp tuyến của đường tròn (𝒞) tại A nên IA ⊥ a hay AC ⊥ a.
Vì đường thẳng c là tiếp tuyến của đường tròn (𝒞) tại C nên IC ⊥ c hay AC ⊥ c.
Do đó a // c hay AE // CF nên tứ giác AEFC là hình thang.
d) Xét đường tròn (𝒞) có:
⦁ hai tiếp tuyến tại A và B lần lượt là a, b cắt nhau tại E nên AE = BE.
⦁ hai tiếp tuyến tại C và B lần lượt là c, b cắt nhau tại F nên CF = BF.
Do đó AE + CF = BE + BF = EF.
Vậy EF = AE + CF.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Kí hiệu ba bạn nam là A, B, C và hai bạn nữ là D, E.
Phép thử là giáo viên chọn ngẫu nhiên hai bạn trong nhóm để tham gia một phong trào của trường.
Kết quả của phép thử là (a, b), trong đó a và b tương ứng là bạn học sinh mà giáo viên lựa chọn.
Vậy không gian mẫu là:
Ω = {(A, B); (A, C); (A, D); (A, E); (B, C); (B, D); (B, E); (C, D); (C, E); (D, E)}.
b) Tập Ω có 10 phần tử.
Vì giáo viên chọn ngẫu nhiên hai bạn trong nhóm nên các kết quả có thể của phép thử là đồng khả năng.
Có 6 kết quả thuận lợi cho biến cố “Hai bạn được chọn khác giới tính” là: (A, D); (A, E); (B, D); (B, E); (C, D); (C, E).
Vậy xác suất để hai bạn được chọn khác giới tính là: \(\frac{6}{{10}} = \frac{3}{5}.\)
Lời giải
Gọi x, y (triệu đồng) lần lượt là số tiền dự tính phải trả vật liệu và công thợ cho mỗi mét vuông xây dựng (0 < x < 600, 0 < y < 600).
+ Theo dự tính, tổng diện tích xây dựng là khoảng 100 m2 nên:
⦁ số tiền dùng để trả vật liệu là: 100x (triệu đồng);
⦁ số tiền dùng để trả công thợ là: 100y (triệu đồng).
Do tổng chi phí (tiền vật liệu và tiền công thợ) chú Ba dự tính hết khoảng 600 triệu đồng nên ta có phương trình:
100x + 100y = 600 hay x + y = 6. (1)
+ Theo thực tế:
⦁ tổng diện tích xây dựng là: 100 + 20 = 120 (m2);
⦁ chi phí tiền vật liệu cho mỗi mét vuông là:
(100% + 10%).x = 1,1x (triệu đồng);
⦁ tiền công thợ cho mỗi mét vuông là:
\(\left( {1 + \frac{1}{5}} \right)y = 1,2y\) (triệu đồng);
⦁ số tiền dùng để trả vật liệu là: 120.1,1x = 132x (triệu đồng);
⦁ số tiền dùng để trả công thợ là: 120.1,2y = 144y (triệu đồng).
Do tổng chi phí thực tế là 804 triệu đồng nên ta có phương trình:
132x + 144y = 804 hay 11x + 12y = 67. (2)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 6\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\11x + 12y = 67\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Nhân hai vế của phương trình (1) với 12, ta được hệ phương trình sau:
\(\left\{ \begin{array}{l}12x + 12y = 72\\11x + 12y = 67.\end{array} \right.\)
Trừ từng vế của hai phương trình trong hệ mới, ta được: x = 5.
Thế x = 5 vào phương trình (1), ta được: 5 + y = 6, suy ra y = 1.
Các giá trị x, y tìm được ở trên đều thỏa mãn điều kiện.
Vậy thực tế chú Ba phải trả 1,1.5 = 5,5 triệu đồng tiền vật liệu và 1,2.1 = 1,2 triệu đồng tiền công thợ cho mỗi mét vuông xây dựng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.